Understanding Variational Autoencoders (VAE) in Neural Networks
Variational Autoencoders (VAEs) are a type of neural network architecture that has gained significant attention in the field of machine learning and artificial intelligence. They are particularly useful for tasks involving generative modeling, where the goal is to generate new data points that resemble a given dataset. VAEs are an extension of traditional autoencoders, with the added benefit of being able to learn complex data distributions.
What is a Variational Autoencoder?
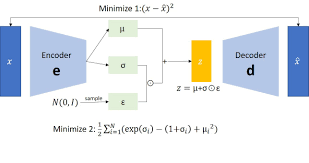
A VAE consists of two main components: an encoder and a decoder. The encoder maps input data into a latent space, while the decoder reconstructs the data from this latent representation. Unlike traditional autoencoders, VAEs introduce probabilistic elements into this process. Instead of mapping inputs to fixed points in latent space, VAEs map them to probability distributions.
The Role of Latent Variables
In VAEs, each input is encoded as a distribution over latent variables rather than as a single point. This allows for capturing more complex patterns and variations within the data. The key idea is to represent each input as a mean and variance, which define a Gaussian distribution in the latent space.
Training a VAE
The training process for VAEs involves optimizing two objectives simultaneously:
- Reconstruction Loss: This measures how well the decoder can reconstruct the original input from its latent representation.
- Kullback-Leibler Divergence (KL Divergence): This ensures that the learned distribution over latent variables is close to a prior distribution, typically a standard normal distribution.
The combination of these objectives allows VAEs to generate new samples by sampling from the learned latent space distributions.
Applications of Variational Autoencoders
VAEs have numerous applications across different domains:
- Image Generation: VAEs can generate realistic images by learning complex features from datasets like faces or landscapes.
- Anomaly Detection: By learning what constitutes “normal” data, VAEs can identify anomalies or outliers effectively.
- Molecular Design: In drug discovery, VAEs help generate novel molecular structures with desired properties.
- NLP Tasks: They can be used for text generation and translation tasks by modeling language patterns.
The Future of VAEs
The development and refinement of variational autoencoders continue to be an exciting area of research. As computational power increases and algorithms become more sophisticated, VAEs are expected to play an even larger role in advancing AI capabilities across various fields. Their ability to model complex distributions makes them invaluable tools for both theoretical research and practical applications.
In conclusion, variational autoencoders represent a significant advancement in neural network architectures with their ability to generate new data points and model intricate patterns within datasets. As research progresses, their potential applications will undoubtedly expand further, offering innovative solutions across diverse industries.
8 Essential Tips for Mastering Variational Autoencoders (VAEs)
- Understand the concept of variational autoencoder (VAE) and how it differs from traditional autoencoders.
- Choose appropriate activation functions for the neural network layers in VAE.
- Implement the reparameterization trick to enable backpropagation through stochastic nodes in VAE.
- Balance the reconstruction loss and KL divergence term in the VAE loss function.
- Regularize the latent space by adding a penalty term to the loss function, such as L2 regularization.
- Experiment with different architectures for the encoder and decoder networks to improve VAE performance.
- Consider annealing strategies for controlling the weight of the KL divergence term during training.
- Evaluate VAE performance using metrics like reconstruction error, latent space visualization, and sample generation quality.
Understand the concept of variational autoencoder (VAE) and how it differs from traditional autoencoders.
To effectively utilize variational autoencoders (VAEs) in neural networks, it is crucial to grasp the fundamental concept of VAEs and comprehend their distinctions from traditional autoencoders. Unlike conventional autoencoders that map inputs to fixed points in latent space, VAEs map inputs to probability distributions. This probabilistic approach allows VAEs to capture complex data patterns by representing each input as a distribution over latent variables rather than a single point. By understanding this key difference, one can harness the power of VAEs to learn intricate data distributions and generate new data points with enhanced flexibility and accuracy.
Choose appropriate activation functions for the neural network layers in VAE.
Selecting suitable activation functions for the neural network layers in a Variational Autoencoder (VAE) is crucial for the model’s performance and efficiency. Since VAEs involve complex probabilistic computations and latent space mappings, the choice of activation functions can significantly impact how well the network learns and represents data distributions. Common choices like ReLU (Rectified Linear Unit) for hidden layers and sigmoid or softmax for output layers are often effective. However, considering the specific requirements of VAEs, using activation functions that preserve gradients during training and promote smooth transformations can enhance the model’s ability to capture intricate patterns in the data distribution. Careful selection of activation functions tailored to the VAE architecture can lead to more stable training, improved reconstruction accuracy, and better generation of new data samples.
Implement the reparameterization trick to enable backpropagation through stochastic nodes in VAE.
To enhance the training efficiency of variational autoencoders (VAEs), implementing the reparameterization trick is crucial. This technique enables backpropagation through stochastic nodes in VAE, allowing for more stable and effective optimization. By decoupling the randomness from the parameters during training, the reparameterization trick ensures that gradients can flow smoothly through the network, facilitating faster convergence and improved model performance. Overall, incorporating this trick enhances the robustness and effectiveness of VAEs in capturing complex data distributions and generating high-quality samples.
Balance the reconstruction loss and KL divergence term in the VAE loss function.
To effectively train a Variational Autoencoder (VAE), it is crucial to strike a balance between the reconstruction loss and the Kullback-Leibler (KL) divergence term in the VAE loss function. The reconstruction loss ensures that the decoder can accurately reconstruct the input data from its latent representation, capturing essential features of the original data. On the other hand, the KL divergence term encourages the learned distribution over latent variables to align with a prior distribution, promoting meaningful and diverse sampling from the latent space. By carefully balancing these two components of the loss function, VAEs can achieve optimal performance in generating new data points while preserving important characteristics of the input data distribution.
Regularize the latent space by adding a penalty term to the loss function, such as L2 regularization.
To enhance the performance and robustness of a Variational Autoencoder (VAE) neural network, it is advisable to regularize the latent space by incorporating a penalty term into the loss function, such as L2 regularization. By adding this regularization term, the VAE is encouraged to learn more meaningful and structured representations in the latent space, which can lead to improved generalization and better control over the generated data points. This regularization technique helps prevent overfitting and promotes a smoother distribution of latent variables, ultimately enhancing the overall quality of the VAE model’s output.
Experiment with different architectures for the encoder and decoder networks to improve VAE performance.
To enhance the performance of a Variational Autoencoder (VAE), it is advisable to explore various architectures for both the encoder and decoder networks. By experimenting with different designs and configurations, researchers and developers can optimize the VAE’s ability to learn complex data distributions and generate more accurate reconstructions. Adjusting the architecture of the encoder can help capture meaningful latent representations, while refining the decoder’s structure can improve the quality of reconstructed outputs. This iterative process of testing different network architectures is crucial in fine-tuning a VAE model for optimal performance across a wide range of applications.
Consider annealing strategies for controlling the weight of the KL divergence term during training.
When implementing a Variational Autoencoder (VAE) neural network, it is crucial to consider annealing strategies to effectively control the weight of the Kullback-Leibler (KL) divergence term during training. Annealing techniques involve gradually adjusting the contribution of the KL divergence term in the overall loss function as training progresses. This approach helps strike a balance between reconstruction accuracy and latent space regularization, ensuring that the model learns meaningful representations while generating diverse and high-quality samples. By incorporating annealing strategies, researchers and developers can optimize the training process of VAEs and improve their performance in various generative modeling tasks.
Evaluate VAE performance using metrics like reconstruction error, latent space visualization, and sample generation quality.
To assess the performance of a Variational Autoencoder (VAE), it is crucial to utilize various metrics that provide insights into different aspects of its functionality. One common metric is the reconstruction error, which measures how accurately the VAE can reconstruct input data from its latent representation. Additionally, visualizing the latent space can offer valuable information about how well the VAE has learned to represent data points in a lower-dimensional space. Furthermore, evaluating sample generation quality can help determine the VAE’s ability to generate new data points that resemble the original dataset. By considering these metrics collectively, one can gain a comprehensive understanding of the VAE’s performance and effectiveness in capturing complex data distributions.