Neural networks have revolutionized the field of artificial intelligence and machine learning, enabling computers to learn complex patterns and make predictions with remarkable accuracy. One area where neural networks are making a significant impact is in solving differential equations, a fundamental concept in mathematics and physics.
Differential equations describe how quantities change over time or space and are used to model a wide range of natural phenomena, from population dynamics to fluid flow. Solving these equations analytically can be challenging or even impossible for complex systems, leading researchers to explore alternative methods such as using neural networks.
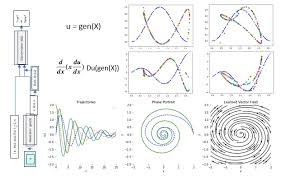
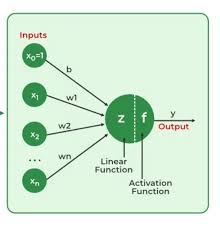
Neural networks are computational models inspired by the structure of the human brain, consisting of interconnected nodes that process and transmit information. By training a neural network on a dataset of input-output pairs derived from a differential equation, the network can learn to approximate the underlying solution.
One common approach is to represent the solution to a differential equation as a neural network architecture, where the input corresponds to the independent variables (e.g., time or position) and the output represents the dependent variables (e.g., temperature or concentration). By adjusting the weights and biases of the network through training, it can learn to predict the behavior of the system over time or space.
Neural networks offer several advantages for solving differential equations. They can handle nonlinearities and high-dimensional systems with ease, making them suitable for a wide range of applications. Additionally, neural networks can adapt to noisy or incomplete data and generalize well to unseen scenarios, providing robust solutions in real-world settings.
Researchers are exploring various techniques to enhance the performance of neural networks in solving differential equations. This includes incorporating physical constraints into the network architecture, leveraging techniques such as residual connections or attention mechanisms, and optimizing hyperparameters through advanced algorithms like stochastic gradient descent.
By combining the power of neural networks with traditional mathematical methods, researchers are pushing the boundaries of what is possible in solving differential equations. The ability to efficiently model complex systems opens up new opportunities for understanding natural phenomena, designing innovative technologies, and advancing scientific knowledge across disciplines.
Exploring Neural Networks and AI in Solving Differential Equations: Top 5 FAQs
- Can AI solve differential equations?
- Can AI do differential equations?
- How to solve an ODE with a neural network?
- How differential equations are used in artificial intelligence?
- How does machine learning solve differential equations?
Can AI solve differential equations?
Yes, AI, particularly through the use of neural networks, can solve differential equations. Neural networks have emerged as a powerful tool for approximating solutions to both ordinary and partial differential equations, especially when traditional analytical methods are not feasible. By training a neural network on data generated from a differential equation, the network can learn to model the underlying system dynamics. This approach is beneficial for handling complex, nonlinear systems or high-dimensional problems that are computationally intensive with conventional methods. Additionally, neural networks can incorporate constraints and adapt to noisy or incomplete data, making them robust in various applications. As a result, AI-driven techniques are increasingly being utilized in fields such as physics, engineering, and finance to solve intricate differential equations efficiently.
Can AI do differential equations?
Artificial intelligence, particularly through the use of neural networks, has shown significant promise in tackling differential equations. While AI doesn’t “do” differential equations in the traditional sense—like a human mathematician might—it can approximate solutions to these equations by learning from data. Neural networks can be trained to recognize patterns and relationships within complex systems described by differential equations, allowing them to predict outcomes and model behaviors without needing explicit analytical solutions. This capability is especially useful for solving nonlinear or high-dimensional differential equations that are challenging with conventional methods. By leveraging AI, researchers and engineers can gain insights into dynamic systems more efficiently, making AI a powerful tool in fields ranging from physics to engineering.
How to solve an ODE with a neural network?
When it comes to solving ordinary differential equations (ODEs) using neural networks, the key lies in training the network to approximate the solution based on input-output pairs derived from the ODE. By representing the ODE solution as a neural network architecture and adjusting the network’s parameters through training, it can learn to predict the behavior of the system over time. This approach allows neural networks to handle nonlinearities and high-dimensional systems effectively, offering a versatile and powerful tool for solving ODEs in various scientific and engineering applications.
How differential equations are used in artificial intelligence?
Differential equations play a crucial role in artificial intelligence by providing a mathematical framework to model and analyze dynamic systems. In the context of neural networks, differential equations are used to describe how the network’s parameters evolve during the training process, allowing researchers to optimize the network’s performance and convergence. By formulating neural network training as an optimization problem governed by differential equations, researchers can leverage tools from dynamical systems theory to understand the behavior of neural networks and improve their training algorithms. This integration of differential equations with artificial intelligence not only enhances the efficiency and robustness of neural network training but also deepens our understanding of the underlying principles governing learning processes in complex systems.
How does machine learning solve differential equations?
Machine learning tackles the challenge of solving differential equations by leveraging neural networks, sophisticated computational models inspired by the human brain. Through training on datasets derived from differential equations, neural networks learn to approximate the solutions to these complex mathematical problems. By representing the differential equation solution as a neural network architecture and adjusting its parameters during training, machine learning enables the network to predict the behavior of systems over time or space. This innovative approach not only handles nonlinearities and high-dimensional systems effectively but also offers robust solutions that can adapt to noisy or incomplete data, demonstrating the power of combining mathematical principles with cutting-edge technology in solving differential equations.