Self-Normalizing Neural Networks: A Breakthrough in Deep Learning
Neural networks have revolutionized the field of artificial intelligence, enabling machines to perform complex tasks with remarkable accuracy. One of the latest advancements in neural network architecture is the development of self-normalizing neural networks (SNNs), which offer significant advantages over traditional architectures.
Unlike conventional neural networks, which often require careful initialization and hyperparameter tuning to prevent issues like vanishing or exploding gradients, SNNs are designed to automatically normalize the activations within each layer. This self-normalization property helps stabilize the training process and accelerates convergence, making SNNs easier to train and more robust.
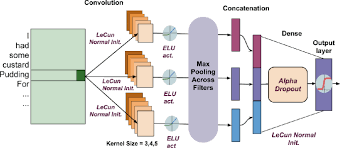
The key innovation behind SNNs is the use of activation functions that have built-in normalization properties, such as the scaled exponential linear unit (SELU) function. When combined with specific weight initialization techniques, such as initializing weights with zero mean and unit variance, SNNs are able to maintain stable activations throughout the network without the need for additional normalization layers or techniques.
Research has shown that SNNs exhibit improved generalization performance, faster convergence rates, and better resistance to overfitting compared to traditional architectures. This makes them particularly well-suited for tasks involving complex data distributions or limited training data, where robustness and efficiency are crucial.
Furthermore, the self-normalizing property of SNNs simplifies the training process and reduces the dependency on manual hyperparameter tuning, making them more accessible to researchers and practitioners alike. As a result, SNNs have gained significant attention in recent years and are being increasingly adopted in various applications across different domains.
In conclusion, self-normalizing neural networks represent a significant advancement in deep learning that addresses key challenges associated with traditional architectures. By automatically normalizing activations and simplifying the training process, SNNs offer a promising solution for improving performance, efficiency, and robustness in neural network models.
Understanding Self-Normalizing Neural Networks: Key Innovations, Advantages, and Impact on Training
- What are self-normalizing neural networks (SNNs) and how do they differ from traditional neural networks?
- What is the key innovation behind self-normalizing neural networks?
- How do self-normalizing neural networks address issues like vanishing or exploding gradients in training?
- What are the advantages of using self-normalizing neural networks in deep learning tasks?
- Are there specific activation functions associated with self-normalizing neural networks?
- How do self-normalizing neural networks impact the training process and convergence rates?
What are self-normalizing neural networks (SNNs) and how do they differ from traditional neural networks?
Self-normalizing neural networks (SNNs) are a cutting-edge advancement in deep learning architecture that sets them apart from traditional neural networks. SNNs are designed to automatically normalize the activations within each layer, eliminating the need for manual normalization techniques or careful hyperparameter tuning. This self-normalization property, achieved through specific activation functions like the scaled exponential linear unit (SELU) and proper weight initialization strategies, helps stabilize training and accelerates convergence. In contrast, traditional neural networks often require additional normalization layers or techniques to prevent issues like vanishing or exploding gradients. The inherent self-normalizing capability of SNNs not only simplifies the training process but also leads to improved generalization performance, faster convergence rates, and enhanced resistance to overfitting, making them a promising choice for various deep learning tasks.
What is the key innovation behind self-normalizing neural networks?
The key innovation behind self-normalizing neural networks lies in their ability to automatically normalize activations within each layer without the need for additional normalization techniques. This is achieved through the use of activation functions, such as the scaled exponential linear unit (SELU), that inherently possess normalization properties. By combining these activation functions with specific weight initialization strategies, self-normalizing neural networks are able to maintain stable activations throughout the network, leading to improved training stability, faster convergence rates, and enhanced generalization performance compared to traditional architectures.
How do self-normalizing neural networks address issues like vanishing or exploding gradients in training?
Self-normalizing neural networks address issues like vanishing or exploding gradients in training by incorporating activation functions with built-in normalization properties, such as the scaled exponential linear unit (SELU) function. By using activation functions that inherently stabilize the activations within each layer, self-normalizing neural networks are able to maintain consistent gradients throughout the network without the need for additional normalization techniques. This self-normalization property helps prevent issues like vanishing or exploding gradients, which can hinder the training process in traditional neural network architectures. As a result, self-normalizing neural networks offer a more stable and efficient training experience, enabling faster convergence rates and improved generalization performance.
What are the advantages of using self-normalizing neural networks in deep learning tasks?
Self-normalizing neural networks offer several advantages in deep learning tasks. One key benefit is their ability to automatically normalize activations within each layer, which helps stabilize the training process and accelerates convergence. This self-normalization property reduces the need for manual hyperparameter tuning and additional normalization techniques, making SNNs easier to train and more robust. Additionally, research has shown that SNNs exhibit improved generalization performance, faster convergence rates, and better resistance to overfitting compared to traditional architectures. These advantages make self-normalizing neural networks a compelling choice for tasks involving complex data distributions or limited training data, where efficiency, robustness, and ease of training are essential considerations.
Are there specific activation functions associated with self-normalizing neural networks?
In the context of self-normalizing neural networks (SNNs), there are specific activation functions that play a crucial role in enabling the self-normalization property of the network. One of the most commonly used activation functions in SNNs is the scaled exponential linear unit (SELU) function, which has inherent normalization properties that help stabilize activations within each layer. By using activation functions like SELU, combined with appropriate weight initialization techniques, SNNs are able to achieve automatic normalization without the need for additional normalization layers or methods. This unique characteristic of specific activation functions in SNNs contributes to their efficiency, robustness, and improved performance in deep learning tasks.
How do self-normalizing neural networks impact the training process and convergence rates?
Self-normalizing neural networks have a profound impact on the training process and convergence rates by introducing automatic normalization of activations within each layer. This inherent self-normalization property helps stabilize the training dynamics, prevent issues like vanishing or exploding gradients, and accelerate convergence towards an optimal solution. By maintaining stable activations throughout the network without the need for additional normalization layers or techniques, self-normalizing neural networks simplify the training process and reduce the dependency on manual hyperparameter tuning. As a result, they exhibit faster convergence rates, improved generalization performance, and enhanced resistance to overfitting compared to traditional architectures, making them highly effective for tasks involving complex data distributions or limited training data.