Linear Neural Network: Understanding the Basics
In the realm of artificial intelligence and machine learning, neural networks are powerful tools that mimic the way the human brain processes information. One fundamental type of neural network is the linear neural network, which serves as a building block for more complex models.
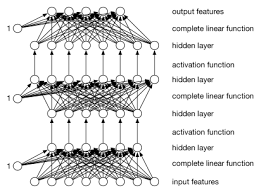
At its core, a linear neural network consists of a series of interconnected nodes, or neurons, organized in layers. Each neuron in one layer is connected to every neuron in the next layer, forming a network that can learn and make predictions based on input data.
The key feature of a linear neural network is its simplicity. In this type of network, each neuron performs a linear operation on its input and passes the result to the next layer without applying any non-linear activation function. This means that the output is a linear combination of the inputs, making it easier to interpret and analyze.
Despite its simplicity, linear neural networks are valuable for tasks that involve linear relationships between variables, such as regression analysis or simple classification problems. They are often used as the first step in building more complex neural networks, where non-linear activation functions are introduced to capture more intricate patterns in the data.
Training a linear neural network involves adjusting the weights assigned to each connection between neurons to minimize the difference between the predicted output and the actual target values. This process, known as gradient descent optimization, allows the network to learn from examples and improve its predictive capabilities over time.
In conclusion, while linear neural networks may seem basic compared to their more sophisticated counterparts, they play a crucial role in machine learning by providing a solid foundation for understanding how neural networks operate and paving the way for more advanced models to tackle complex tasks.
6 Essential Tips for Building Effective Linear Neural Networks
- Start by defining the input layer based on the number of features in your dataset.
- Choose an appropriate activation function for the hidden layers, such as ReLU or sigmoid.
- Initialize the weights and biases randomly to break symmetry and prevent vanishing gradients.
- Use an optimizer like Stochastic Gradient Descent (SGD) or Adam to update weights during training.
- Monitor the loss function to track how well the model is learning and make adjustments as needed.
- Consider adding regularization techniques like L1 or L2 regularization to prevent overfitting.
Start by defining the input layer based on the number of features in your dataset.
When building a linear neural network, it is essential to start by defining the input layer based on the number of features present in your dataset. The input layer serves as the initial point where data is fed into the network for processing. By accurately specifying the input layer dimensions to match the number of features in your dataset, you ensure that the network can effectively capture and analyze all relevant information during training and prediction tasks. This foundational step sets the stage for proper data representation and efficient learning within the neural network architecture.
Choose an appropriate activation function for the hidden layers, such as ReLU or sigmoid.
When working with a linear neural network, it is essential to select the right activation function for the hidden layers to enhance the network’s performance. Popular choices like ReLU (Rectified Linear Unit) or sigmoid functions can introduce non-linearity and enable the network to learn complex patterns in the data. ReLU is commonly preferred for its simplicity and effectiveness in addressing the vanishing gradient problem, while sigmoid functions are useful for binary classification tasks. By carefully choosing an appropriate activation function, such as ReLU or sigmoid, for the hidden layers of a linear neural network, you can improve its ability to capture intricate relationships within the data and enhance overall predictive accuracy.
Initialize the weights and biases randomly to break symmetry and prevent vanishing gradients.
To enhance the performance of a linear neural network, it is crucial to initialize the weights and biases randomly. This practice helps break symmetry within the network and prevents issues like vanishing gradients during training. By starting with random values for weights and biases, the network can explore different paths and avoid getting stuck in suboptimal solutions. This initialization strategy promotes better learning dynamics and enables the network to effectively adapt to the complexities of the data, ultimately improving its overall predictive accuracy and performance.
Use an optimizer like Stochastic Gradient Descent (SGD) or Adam to update weights during training.
To enhance the training process of a linear neural network, it is advisable to utilize an optimizer such as Stochastic Gradient Descent (SGD) or Adam. These optimization algorithms play a crucial role in updating the weights of the network during training by efficiently adjusting them to minimize the difference between predicted and actual values. By incorporating SGD or Adam, the network can navigate through the vast parameter space more effectively, leading to faster convergence and improved performance in learning linear relationships within the data.
Monitor the loss function to track how well the model is learning and make adjustments as needed.
Monitoring the loss function is a critical tip when working with a linear neural network. The loss function serves as a measure of how well the model is learning from the training data, indicating the discrepancy between the predicted output and the actual target values. By tracking the loss function during training, developers can assess the performance of the model and make necessary adjustments to improve its accuracy and predictive capabilities. This iterative process of monitoring and adjusting helps optimize the network’s learning process and enhances its ability to make accurate predictions on new data.
Consider adding regularization techniques like L1 or L2 regularization to prevent overfitting.
To enhance the performance of a linear neural network and prevent overfitting, it is advisable to incorporate regularization techniques such as L1 or L2 regularization. By adding these techniques, the model can effectively control the complexity of the network and reduce the risk of fitting noise in the training data. L1 regularization encourages sparsity in the weights by penalizing large coefficients, while L2 regularization limits the magnitude of the weights to prevent them from becoming too large. Implementing these regularization methods can help improve the generalization ability of the linear neural network and make it more robust when dealing with unseen data.