Neural Network Linear Regression: Understanding the Basics
Neural networks have revolutionized the field of machine learning by enabling complex computations and pattern recognition. One fundamental concept in neural networks is linear regression, which serves as a building block for more advanced models.
Linear regression is a simple yet powerful technique used to model the relationship between a dependent variable and one or more independent variables. In the context of neural networks, linear regression involves predicting an output value based on input features by finding the best-fitting line that minimizes the error.
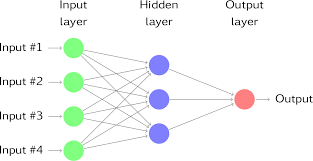
Neural network linear regression extends traditional linear regression by incorporating multiple layers of interconnected nodes, or neurons, that perform nonlinear transformations on the input data. These layers allow neural networks to capture complex patterns and relationships in the data that may not be discernible through linear models alone.
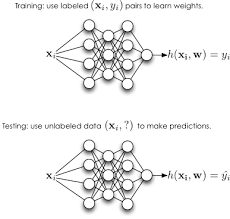
The process of training a neural network for linear regression involves feeding input data through the network, adjusting the weights and biases of each neuron based on the error between predicted and actual output values, and iteratively optimizing these parameters to minimize prediction errors.
By leveraging neural network linear regression, researchers and practitioners can tackle a wide range of prediction tasks, from stock market forecasting to medical diagnosis. The flexibility and adaptability of neural networks make them well-suited for handling diverse datasets and extracting valuable insights from complex data structures.
In conclusion, neural network linear regression represents a foundational concept in machine learning that underpins more advanced neural network architectures. By understanding the principles behind this technique, practitioners can harness the power of neural networks to solve real-world problems and drive innovation across various industries.
9 Essential Tips for Effective Neural Network Linear Regression
- Understand the basics of linear regression and how it applies to neural networks.
- Ensure your data is properly preprocessed before training the neural network for linear regression.
- Choose an appropriate loss function such as Mean Squared Error for linear regression tasks.
- Select a suitable optimizer like Stochastic Gradient Descent to minimize the loss during training.
- Regularize your neural network using techniques like L1 or L2 regularization to prevent overfitting.
- ‘Batch size’ and ‘learning rate’ are hyperparameters that significantly affect training in neural network linear regression.
- ‘Feature scaling’ can help improve convergence and speed up training in neural network linear regression.
- ‘Early stopping’ can prevent overfitting and improve generalization performance in neural network linear regression.
- ‘Visualizing the learned weights’ can provide insights into how each feature contributes to the prediction in a neural network for linear regression.
Understand the basics of linear regression and how it applies to neural networks.
To effectively utilize neural network linear regression, it is crucial to grasp the fundamentals of linear regression and its relevance within neural networks. By comprehending the principles of linear regression, including how it models the relationship between variables and minimizes errors, individuals can better appreciate how neural networks leverage this technique to make predictions and extract valuable insights from complex datasets. Understanding the foundational concepts of linear regression is key to unlocking the full potential of neural network applications in various fields, from finance to healthcare.
Ensure your data is properly preprocessed before training the neural network for linear regression.
Before training a neural network for linear regression, it is crucial to ensure that your data is properly preprocessed. Data preprocessing involves tasks such as handling missing values, normalizing or standardizing features, and encoding categorical variables. By preparing your data effectively, you can improve the performance and accuracy of the neural network model. Properly preprocessed data helps the neural network learn patterns and relationships more effectively, leading to more reliable predictions and insights. Investing time in data preprocessing before training your neural network for linear regression can ultimately enhance the quality of your results and optimize the overall performance of your model.
Choose an appropriate loss function such as Mean Squared Error for linear regression tasks.
When working on neural network linear regression tasks, it is crucial to select the right loss function to optimize the model effectively. One commonly used loss function for linear regression is Mean Squared Error (MSE), which calculates the average of the squared differences between predicted and actual values. By choosing MSE as the loss function, the neural network aims to minimize this error during training, leading to more accurate predictions and a better-fitting model for linear regression tasks. Making informed decisions about loss functions like MSE can significantly impact the performance and success of neural network models in handling regression problems.
Select a suitable optimizer like Stochastic Gradient Descent to minimize the loss during training.
When working with neural network linear regression, it is crucial to select a suitable optimizer like Stochastic Gradient Descent to minimize the loss function during training. Optimizers play a key role in adjusting the weights and biases of the neural network to improve its performance by reducing prediction errors. Stochastic Gradient Descent is particularly effective for large datasets, as it updates the model parameters based on small batches of data rather than the entire dataset at once, leading to faster convergence and more efficient training. By choosing the right optimizer, such as Stochastic Gradient Descent, practitioners can enhance the learning process of their neural network models and achieve better results in predictive tasks.
Regularize your neural network using techniques like L1 or L2 regularization to prevent overfitting.
To enhance the performance and generalization of your neural network model in linear regression tasks, it is crucial to incorporate regularization techniques such as L1 or L2 regularization. By applying regularization, you can effectively prevent overfitting, a common issue where the model performs well on training data but fails to generalize to unseen data. L1 regularization encourages sparsity in the model by penalizing large weight values, while L2 regularization controls the complexity of the model by adding a penalty term to the loss function based on the squared magnitude of weights. By regularizing your neural network using these techniques, you can improve its robustness and ensure that it learns meaningful patterns from the data without memorizing noise or outliers.
‘Batch size’ and ‘learning rate’ are hyperparameters that significantly affect training in neural network linear regression.
The choice of ‘batch size’ and ‘learning rate’ are critical hyperparameters that have a significant impact on the training process in neural network linear regression. The batch size determines the number of data points processed in each iteration, affecting the speed and stability of training. On the other hand, the learning rate controls the size of the step taken during optimization, influencing how quickly the model converges to an optimal solution. Finding the right balance between batch size and learning rate is essential for achieving efficient and effective training results in neural network linear regression models.
‘Feature scaling’ can help improve convergence and speed up training in neural network linear regression.
Implementing ‘feature scaling’ is a crucial tip to enhance convergence and accelerate training in neural network linear regression. By normalizing the range of input features to a consistent scale, such as between 0 and 1 or -1 and 1, feature scaling can prevent certain features from dominating the learning process due to their larger magnitudes. This practice not only improves the efficiency of gradient descent optimization but also aids in achieving faster convergence towards an optimal solution. Overall, incorporating feature scaling in neural network linear regression can significantly enhance model performance and training speed.
‘Early stopping’ can prevent overfitting and improve generalization performance in neural network linear regression.
Implementing ‘early stopping’ in neural network linear regression can be a crucial strategy to prevent overfitting and enhance generalization performance. By monitoring the model’s performance on a validation dataset during training and halting the training process when the validation error starts to increase, ‘early stopping’ helps prevent the neural network from memorizing noise in the training data and ensures that it learns meaningful patterns that can be generalized to unseen data. This technique not only improves the model’s ability to make accurate predictions on new data but also promotes efficiency by avoiding unnecessary training iterations that could lead to overfitting.
‘Visualizing the learned weights’ can provide insights into how each feature contributes to the prediction in a neural network for linear regression.
Visualizing the learned weights in a neural network for linear regression can offer valuable insights into the contribution of each feature towards the prediction process. By examining the weights assigned to different features, researchers and data scientists can gain a deeper understanding of which variables are influencing the model’s output and to what extent. This visualization technique not only helps in interpreting the inner workings of the neural network but also aids in identifying important features, detecting potential biases, and refining the model for improved performance and accuracy.