Understanding Single Hidden Layer Neural Networks
Neural networks are a cornerstone of modern artificial intelligence, powering everything from image recognition systems to language translation tools. Among the various architectures, the single hidden layer neural network is a fundamental concept that provides insight into how more complex networks operate.
What is a Single Hidden Layer Neural Network?
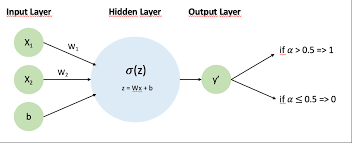
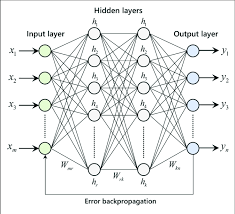
A single hidden layer neural network consists of three main components: an input layer, one hidden layer, and an output layer. Each layer is made up of nodes, also known as neurons. The input layer receives the initial data, the hidden layer processes this information through weighted connections and activation functions, and the output layer produces the final result.
The Role of the Hidden Layer
The hidden layer is crucial for capturing complex patterns in data. It acts as an intermediary between input and output layers by transforming inputs into outputs through non-linear transformations. This transformation allows the network to learn intricate relationships within the data that simple linear models cannot capture.
Activation Functions
Activation functions introduce non-linearity into the model, enabling it to learn from errors and adjust accordingly. Common activation functions used in single hidden layer networks include:
- Sigmoid: Outputs values between 0 and 1, often used for binary classification tasks.
- Tanh: Outputs values between -1 and 1, providing stronger gradients than sigmoid functions.
- ReLU (Rectified Linear Unit): Outputs zero for negative inputs and a linear function for positive inputs, helping to mitigate issues like vanishing gradients.
Training a Single Hidden Layer Neural Network
The training process involves adjusting weights associated with connections between neurons to minimize prediction error. This is typically achieved using algorithms like backpropagation combined with optimization techniques such as gradient descent.
- Forward Propagation: Input data passes through each layer of the network to generate predictions.
- Error Calculation: The difference between predicted outputs and actual target values is calculated using a loss function.
- Backward Propagation: Errors are propagated backward through the network to update weights based on their contribution to total error.
The Power and Limitations of Single Hidden Layer Networks
A single hidden layer neural network can approximate any continuous function given enough neurons in its hidden layer—a concept known as the universal approximation theorem. However, its practical capability may be limited by factors such as computational resources or overfitting when too many neurons are used without sufficient data or regularization techniques.
Conclusion
The single hidden layer neural network serves as an essential building block for understanding more complex architectures like deep neural networks with multiple layers. By mastering this fundamental concept, one gains valuable insights into how machines can learn from data to perform tasks ranging from simple predictions to sophisticated decision-making processes.
Five Key Advantages of Single Hidden Layer Neural Networks: Simplicity, Efficiency, Interpretability, Generalization, and Universal Approximation
Challenges of Single Hidden Layer Neural Networks: Complexity, Overfitting, Gradient Issues, Depth Limitations, and Non-linear Separability
- Limited complexity
- Overfitting risk
- Gradient vanishing/exploding
- Lack of depth hierarchy
- Difficulty with non-linear separability
Simplicity
One significant advantage of single hidden layer neural networks is their simplicity. Unlike deeper architectures, single hidden layer networks are easier to grasp and implement, making them an excellent starting point for beginners in neural network programming. With fewer layers to manage and fewer parameters to tune, individuals new to the field can quickly gain a foundational understanding of how neural networks function without getting overwhelmed by complexity. This simplicity not only accelerates the learning curve but also allows for a more straightforward troubleshooting process, enabling beginners to focus on mastering the fundamental principles of neural network design and training.
Efficiency
Single hidden layer neural networks offer the advantage of efficiency, requiring fewer computational resources and less training time in comparison to deeper networks. This characteristic makes them particularly well-suited for tasks where speed is a critical factor. By simplifying the network architecture and reducing the complexity of calculations, single hidden layer networks can deliver quick results without compromising on performance, making them a practical choice for applications that demand rapid processing and decision-making capabilities.
Interpretability
The pro of interpretability in a single hidden layer neural network lies in its simplicity, making it easier to understand how the network analyzes data and generates predictions. By having fewer layers, the flow of information from input to output is more transparent, allowing stakeholders to gain insights into the decision-making process. This enhanced interpretability not only promotes trust in the model’s outputs but also facilitates adjustments and improvements based on a clear understanding of how the network operates.
Generalization
One significant advantage of single hidden layer neural networks is their ability to generalize effectively on simpler datasets without succumbing to overfitting. By striking a balance between capturing essential patterns in the data and avoiding memorization of noise, these networks exhibit robust performance across a diverse set of tasks. This inherent capability to generalize well enables single hidden layer networks to deliver reliable results and maintain consistency even when faced with varying input conditions, making them versatile and valuable tools in the realm of artificial intelligence applications.
Universal Approximation Theorem
The Universal Approximation Theorem highlights a significant advantage of single hidden layer neural networks: their ability to approximate any continuous function when equipped with an adequate number of neurons in the hidden layer. This remarkable capability underscores the network’s versatility in modeling intricate and complex relationships within data, showcasing its potential to adapt and learn from diverse datasets effectively. By leveraging this theorem, single hidden layer neural networks demonstrate their power to handle a wide range of tasks that involve capturing nuanced patterns and structures, making them a valuable tool in various fields of artificial intelligence and machine learning.
Limited complexity
Single hidden layer neural networks may face limitations in capturing highly intricate patterns within data when compared to deeper architectures. Due to the restricted depth of the network, complex relationships and nuances present in the data may not be effectively captured by a single hidden layer, leading to potential challenges in accurately representing and learning from intricate patterns. Deeper architectures with multiple hidden layers have the advantage of hierarchically extracting features at different levels of abstraction, allowing for more nuanced understanding and representation of complex data structures.
Overfitting risk
One significant drawback of a single hidden layer neural network is the increased risk of overfitting the training data when the number of neurons is limited. Overfitting occurs when the model learns noise and irrelevant patterns in the training data, resulting in excellent performance on the training set but poor generalization to unseen data. With fewer neurons available to capture the complexity of the underlying data distribution, the network may struggle to generalize well beyond the training examples, compromising its ability to make accurate predictions in real-world scenarios. This limitation highlights the importance of carefully balancing model complexity and dataset size to mitigate the risk of overfitting in single hidden layer networks.
Gradient vanishing/exploding
Training a single hidden layer neural network can present challenges such as gradient vanishing or exploding, particularly when using certain activation functions. The phenomenon of vanishing gradients occurs when the gradients become extremely small as they propagate backward through the network during training, leading to slow learning or stagnation. On the other hand, exploding gradients result in excessively large gradient values, causing instability and hindering convergence. These issues can make it difficult to effectively optimize the network’s parameters and may require careful selection of activation functions and initialization methods to mitigate gradient-related problems.
Lack of depth hierarchy
One significant drawback of single hidden layer neural networks is their lack of depth hierarchy, which sets them apart from deeper architectures. The absence of multiple layers in a single hidden layer network can restrict its capacity to learn hierarchical features effectively. Deeper networks with multiple hidden layers have the advantage of capturing increasingly complex patterns and representations through a hierarchy of features, allowing for more nuanced and sophisticated learning capabilities. In contrast, the shallow structure of single hidden layer networks may hinder their ability to extract intricate hierarchical relationships within the data, potentially limiting their overall learning capacity and performance in tasks that require hierarchical feature extraction.
Difficulty with non-linear separability
One significant drawback of a single hidden layer neural network is its limitation in handling complex datasets that demand non-linear decision boundaries. In cases where the data points are not linearly separable, meaning they cannot be effectively classified using straight lines or planes, a single hidden layer network may struggle to capture the intricate relationships within the data. This difficulty with non-linear separability can result in suboptimal performance and reduced accuracy when dealing with datasets that exhibit complex patterns and structures that cannot be adequately represented by a single hidden layer architecture.