Understanding Linear Layer Neural Networks
Neural networks have become a cornerstone of modern artificial intelligence and machine learning applications. Among the various components that make up these complex systems, the linear layer stands out as one of the most fundamental building blocks. This article delves into the concept of linear layer neural networks, explaining what they are, how they function, and their significance in machine learning.
What is a Linear Layer?
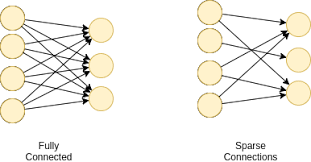
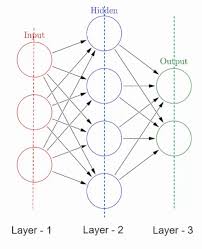
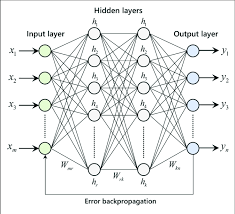
A linear layer, also known as a fully connected layer or dense layer, is a basic type of layer in a neural network where each input node is connected to each output node by a weight. Mathematically, it performs a linear transformation on the input data:
y = Wx + bHere:
- x represents the input vector.
- W is the weight matrix.
- b is the bias vector.
- y is the output vector.
The goal of this transformation is to map the input features to outputs that can be used for prediction or further processing in subsequent layers.
The Role of Weights and Biases
The weights and biases are crucial parameters within a linear layer. They determine how each input feature influences each output feature. During training, these parameters are adjusted to minimize the error between predicted outputs and actual outputs (labels). This process involves an optimization algorithm such as gradient descent.
Weights (W)
The weight matrix (W) defines how strongly each input feature contributes to each output feature. If there are N inputs and M outputs, then (W) will be an MxN matrix.
Biases (b)
The bias vector (b), adds an additional degree of freedom to the model by allowing it to fit data even when all inputs are zero. It helps in shifting the activation function left or right which can be crucial for learning complex patterns.
The Activation Function: Adding Non-Linearity
A purely linear transformation might not be sufficient for capturing complex patterns in data. Therefore, after applying a linear transformation using weights and biases, an activation function is often applied to introduce non-linearity into the model. Common activation functions include ReLU (Rectified Linear Unit), sigmoid, and tanh functions.
a = f(y)This step ensures that neural networks can learn more intricate relationships between inputs and outputs rather than being limited to simple linear mappings.
The Importance of Linear Layers in Neural Networks
The simplicity and flexibility of linear layers make them indispensable in various types of neural networks including feedforward neural networks (FNNs), convolutional neural networks (CNNs), recurrent neural networks (RNNs), among others:
- Simplicity:: The mathematical operations involved in a linear layer are straightforward yet powerful enough for many tasks.
- Diversity:: They can be used as building blocks for more complex architectures like deep neural networks.
- Efficacy:: Combined with other types of layers such as convolutional or recurrent layers; they significantly enhance model performance on tasks like image recognition or natural language processing.
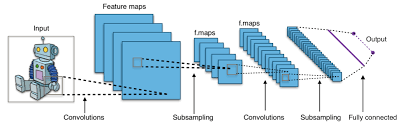
A Practical Example: Image Classification with Linear Layers
: Consider an image classification task where we aim to classify images into different categories.:
After passing through several convolutional layers that extract spatial features from images;
the resulting feature maps may be flattened into vectors which serve as inputs into one or more fully connected (linear) layers before making final predictions through softmax function at output layer.:
This combination allows us not only capture spatial hierarchies but also learn high-level representations required for accurate classification.:
In summary;
linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know exactly refers its pivotal role shaping intelligent systems around us.:
Happy Learning!:
Conclusion
Linear-layer-neural-networks form backbone many sophisticated AI models today owing their simplicity;
flexibility;
efficacy combining other advanced techniques enable tackle wide range real-world problems effectively efficiently.: Understanding working principles behind these layers essential anyone looking delve deeper field machine learning artificial intelligence.: So next time encounter term “linear-layer” know
Understanding Linear Layers in Neural Networks: Top 8 Frequently Asked Questions
- Is linear layer same as fully connected layer?
- Why do we use linear layers?
- What are linear layers in neural networks?
- What is a linear function in neural network?
- What does linear layer mean?
- What is a linear model in a neural network?
- What is a linear layer in neural networks?
- What is the difference between linear and non-linear neural networks?
Is linear layer same as fully connected layer?
The frequently asked question about linear layer neural networks often revolves around whether a linear layer is the same as a fully connected layer. In the context of neural networks, these terms are used interchangeably to refer to a type of layer where each input node is connected to each output node by a weight. This connectivity pattern allows for a direct mapping of input features to output features through a linear transformation. Therefore, in practical terms, when discussing neural network architectures and implementations, linear layers and fully connected layers are typically considered synonymous and serve as essential components in building effective machine learning models.
Why do we use linear layers?
Linear layers are a fundamental component of neural networks due to their simplicity, flexibility, and efficacy in capturing complex patterns in data. We use linear layers because they enable straightforward mathematical operations that map input features to output predictions. These layers serve as building blocks for more advanced architectures, allowing neural networks to learn intricate relationships between inputs and outputs. Additionally, the weights and biases within linear layers are crucial parameters that can be adjusted during training to minimize prediction errors. By incorporating non-linear activation functions after linear transformations, we can introduce complexity and depth to neural network models, making them capable of handling a wide range of real-world problems effectively and efficiently.
What are linear layers in neural networks?
Linear layers in neural networks are fundamental components that play a crucial role in transforming input data into meaningful output. Essentially, linear layers perform a linear transformation on the input features using weights and biases, mapping them to the desired output space. Each input node is connected to each output node through a weight matrix, with an additional bias term for added flexibility. These layers are essential for capturing relationships between different features in the data and serve as the building blocks for more complex neural network architectures. By understanding the concept of linear layers, one can grasp how neural networks learn and make predictions based on the patterns present in the input data.
What is a linear function in neural network?
In the context of neural networks, a linear function refers to a simple mathematical operation where each input feature is multiplied by a weight and then summed up with a bias term. This process results in a linear transformation of the input data. In a neural network, a linear function is typically represented by a linear layer, also known as a fully connected layer or dense layer. The purpose of applying linear functions in neural networks is to map the input features to output values that can be used for prediction or further processing in subsequent layers. While linear functions are essential building blocks in neural networks, they are often followed by non-linear activation functions to enable the model to learn complex patterns and relationships in the data.
What does linear layer mean?
The term “linear layer” in the context of neural networks refers to a fundamental component that performs a linear transformation on input data. In simple terms, a linear layer connects every input node to every output node through a set of weights and biases. This transformation is represented mathematically as y = Wx + b, where x is the input vector, W is the weight matrix, b is the bias vector, and y is the output vector. The purpose of a linear layer is to map input features to output features by adjusting the weights and biases during training to minimize errors. While linear layers provide essential building blocks for neural networks, they are often followed by activation functions to introduce non-linearity and enable the network to learn complex patterns in data.
What is a linear model in a neural network?
A linear model in a neural network refers to a basic type of layer where each input node is connected to each output node by a weight, performing a linear transformation on the input data. In this setup, the output is calculated as the sum of the weighted inputs plus a bias term. The purpose of a linear model is to map input features to output predictions effectively. While simple in structure, linear models play a crucial role in neural networks by providing foundational building blocks for more complex architectures, enabling the network to learn and make predictions based on the relationships between input features and target outputs.
What is a linear layer in neural networks?
A linear layer in neural networks, also known as a fully connected layer or dense layer, plays a crucial role in transforming input data through a linear operation involving weights and biases. Essentially, each input node is connected to each output node via weighted connections, with an added bias term. This linear transformation is fundamental in mapping input features to output predictions within the network. The weights determine the strength of influence of each input feature on the outputs, while biases provide additional flexibility to the model. Together, these components form the backbone of neural network architectures, enabling them to learn complex patterns and relationships in data for various machine learning tasks.
What is the difference between linear and non-linear neural networks?
A frequently asked question in the realm of neural networks is: What is the difference between linear and non-linear neural networks? Linear neural networks, characterized by their simple linear transformations from input to output using weights and biases, are limited to capturing linear relationships in data. On the other hand, non-linear neural networks incorporate activation functions after linear transformations, allowing them to model complex, non-linear patterns and relationships within the data. This added flexibility enables non-linear neural networks to learn and represent more intricate structures, making them more suitable for tasks that involve capturing nuanced and nonlinear patterns in data.