Deep Sparse Rectifier Neural Networks: Unleashing the Power of Sparse Representations
In the realm of artificial intelligence and machine learning, deep neural networks have revolutionized the way we approach complex problems. Among the various types of neural networks, deep sparse rectifier neural networks have emerged as a powerful tool for learning intricate patterns and representations from data.
What sets deep sparse rectifier neural networks apart is their ability to learn sparse representations of data. Unlike traditional neural networks that tend to learn dense and redundant representations, sparse rectifier networks focus on capturing only the most essential features of the input data. This not only leads to more efficient use of computational resources but also enhances the interpretability and generalization capabilities of the model.
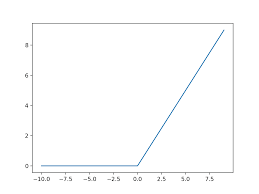
The “rectifier” in deep sparse rectifier neural networks refers to the rectified linear unit (ReLU) activation function, which is commonly used in each neuron of the network. ReLU introduces non-linearity into the network by allowing neurons to activate only when their input exceeds a certain threshold, effectively sparsifying the network’s activations. This sparsity encourages neurons to specialize in detecting specific features, leading to a more disentangled and informative representation of the data.
One of the key advantages of deep sparse rectifier neural networks is their ability to handle high-dimensional data with ease. By learning sparse representations, these networks can effectively compress information while preserving important details, making them well-suited for tasks such as image recognition, natural language processing, and anomaly detection.
Moreover, deep sparse rectifier neural networks have been shown to exhibit better generalization performance compared to their dense counterparts. The sparsity induced by ReLU helps prevent overfitting by promoting feature selection and reducing noise in the learned representations. This results in models that are more robust and capable of adapting to new data with minimal loss in performance.
In conclusion, deep sparse rectifier neural networks represent a significant advancement in the field of deep learning. By harnessing the power of sparse representations and leveraging the non-linearity introduced by ReLU activations, these networks offer a compelling solution for tackling complex real-world problems efficiently and effectively.
Understanding Deep Sparse Rectifier Neural Networks: Key Questions and Insights
- What are deep sparse rectifier neural networks?
- How do deep sparse rectifier neural networks differ from traditional neural networks?
- What is the significance of learning sparse representations in deep sparse rectifier neural networks?
- Why is the rectified linear unit (ReLU) activation function commonly used in deep sparse rectifier neural networks?
- In what types of tasks are deep sparse rectifier neural networks particularly effective?
- What advantages do deep sparse rectifier neural networks offer for handling high-dimensional data?
- How do deep sparse rectifier neural networks prevent overfitting and improve generalization performance?
- Can you provide examples of real-world applications where deep sparse rectifier neural networks have been successfully employed?
- What makes deep sparse rectifier neural networks a compelling choice for complex problem-solving in machine learning and artificial intelligence?
What are deep sparse rectifier neural networks?
Deep sparse rectifier neural networks are a specialized type of neural network that stands out for its ability to learn sparse representations of data. Unlike traditional neural networks that often capture dense and redundant features, deep sparse rectifier networks focus on identifying and utilizing only the most essential aspects of the input data. By incorporating rectified linear units (ReLU) as activation functions, these networks encourage sparsity in their activations, enabling neurons to specialize in detecting specific features. This emphasis on sparsity not only enhances computational efficiency but also improves interpretability and generalization capabilities, making deep sparse rectifier neural networks a powerful tool for complex pattern recognition tasks.
How do deep sparse rectifier neural networks differ from traditional neural networks?
Deep sparse rectifier neural networks differ from traditional neural networks in their approach to learning representations from data. While traditional neural networks tend to learn dense and redundant representations, deep sparse rectifier neural networks focus on capturing sparse and informative features. This is achieved through the use of rectified linear units (ReLU) as activation functions, which introduce sparsity by only activating neurons when their input exceeds a certain threshold. This emphasis on sparsity allows deep sparse rectifier neural networks to specialize in detecting specific features, leading to more efficient use of computational resources, enhanced interpretability, and improved generalization capabilities compared to traditional dense neural networks.
What is the significance of learning sparse representations in deep sparse rectifier neural networks?
Learning sparse representations in deep sparse rectifier neural networks holds significant importance in enhancing the efficiency, interpretability, and generalization capabilities of the model. By focusing on capturing only the most essential features of the input data, these networks can effectively reduce redundancy and noise in the learned representations. This sparsity not only allows for more efficient use of computational resources but also promotes better feature selection, leading to a more disentangled and informative representation of the data. Moreover, the sparse nature of these representations helps prevent overfitting and improves the model’s ability to generalize well to unseen data, making deep sparse rectifier neural networks a powerful tool for handling high-dimensional data and complex learning tasks with precision and effectiveness.
Why is the rectified linear unit (ReLU) activation function commonly used in deep sparse rectifier neural networks?
The rectified linear unit (ReLU) activation function is commonly used in deep sparse rectifier neural networks due to its ability to introduce non-linearity and sparsity into the network. By allowing neurons to activate only when their input surpasses a certain threshold, ReLU promotes sparse activations, where only a subset of neurons are active at any given time. This sparsity encourages the network to focus on learning essential features and reduces redundancy in the learned representations. Additionally, the non-linear nature of ReLU enables deep sparse rectifier neural networks to capture complex patterns and relationships in the data, leading to more efficient learning and improved generalization performance.
In what types of tasks are deep sparse rectifier neural networks particularly effective?
Deep sparse rectifier neural networks are particularly effective in tasks that involve handling high-dimensional data and require learning intricate patterns and representations. These networks excel in tasks such as image recognition, natural language processing, and anomaly detection, where the ability to capture sparse and essential features from complex data is crucial. By promoting sparsity through the rectified linear unit (ReLU) activation function, deep sparse rectifier neural networks can efficiently compress information while preserving important details, leading to more interpretable and generalizable models. Their enhanced generalization performance makes them well-suited for tasks that demand robustness and adaptability to new data with minimal loss in performance.
What advantages do deep sparse rectifier neural networks offer for handling high-dimensional data?
Deep sparse rectifier neural networks offer several advantages for handling high-dimensional data. By learning sparse representations of the input data, these networks can effectively compress information while preserving important details, making them well-suited for tasks involving complex and large datasets. The sparsity induced by the rectified linear unit (ReLU) activation function encourages neurons to specialize in detecting specific features, leading to a more efficient use of computational resources and enhanced interpretability of the learned representations. This capability not only improves the model’s performance in tasks such as image recognition and natural language processing but also helps prevent overfitting and noise in the learned representations, resulting in more robust and generalizable models for high-dimensional data analysis.
How do deep sparse rectifier neural networks prevent overfitting and improve generalization performance?
Deep sparse rectifier neural networks prevent overfitting and enhance generalization performance through the utilization of sparse representations and the rectified linear unit (ReLU) activation function. By encouraging neurons to activate only when their input surpasses a certain threshold, ReLU promotes sparsity in the network’s activations, allowing for more focused and specialized feature detection. This sparsity helps prevent the network from memorizing noise in the training data, leading to improved generalization to unseen data. Additionally, the sparse representations learned by deep sparse rectifier neural networks facilitate effective feature selection, reducing model complexity and enhancing its ability to capture essential patterns in the data while avoiding overfitting.
Can you provide examples of real-world applications where deep sparse rectifier neural networks have been successfully employed?
Deep sparse rectifier neural networks have found successful applications across various domains, showcasing their versatility and effectiveness in real-world scenarios. In the field of computer vision, these networks have been utilized for tasks such as image classification, object detection, and facial recognition. For instance, deep sparse rectifier neural networks have been employed in medical imaging to assist in the diagnosis of diseases from MRI scans and X-rays with high accuracy. In natural language processing, these networks have been used for sentiment analysis, machine translation, and text summarization tasks. Additionally, in the financial sector, deep sparse rectifier neural networks have shown promise in predicting stock prices and detecting fraudulent transactions. Overall, the adaptability and performance of deep sparse rectifier neural networks make them a valuable tool for a wide range of practical applications with significant impact.
What makes deep sparse rectifier neural networks a compelling choice for complex problem-solving in machine learning and artificial intelligence?
Deep sparse rectifier neural networks stand out as a compelling choice for complex problem-solving in machine learning and artificial intelligence due to their unique ability to learn sparse representations of data. By focusing on capturing only the most essential features of the input data, these networks promote efficiency, interpretability, and generalization in model learning. The incorporation of rectified linear units (ReLU) as activation functions introduces sparsity into the network, encouraging neurons to specialize in detecting specific features and enhancing the network’s ability to handle high-dimensional data effectively. This emphasis on sparsity not only aids in compressing information while preserving crucial details but also contributes to better generalization performance by reducing overfitting and noise in learned representations. Overall, deep sparse rectifier neural networks offer a powerful solution for addressing complex problems by leveraging sparse representations and non-linear activations to achieve robust and efficient learning outcomes.