Bayesian Neural Network: Combining the Power of Neural Networks and Bayesian Inference
Neural networks have revolutionized the field of artificial intelligence, enabling machines to learn complex patterns and make predictions based on vast amounts of data. On the other hand, Bayesian inference provides a powerful framework for reasoning under uncertainty, allowing us to quantify our beliefs about unknown variables.
What if we could combine the strengths of neural networks and Bayesian inference into a single model? Enter the Bayesian neural network (BNN), a cutting-edge approach that merges these two powerful paradigms to create a more robust and flexible machine learning system.
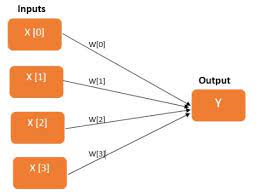
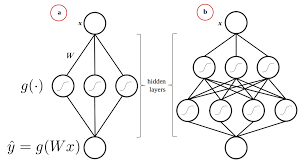
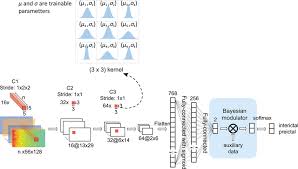
At its core, a Bayesian neural network is similar to a traditional neural network, with layers of interconnected nodes that process input data and produce output predictions. However, in a BNN, each weight and bias parameter in the network is assigned a probability distribution instead of a fixed value.
This probabilistic approach allows the model to capture uncertainty in its predictions and make more reliable estimates of its own confidence. By treating weights as random variables, BNNs can provide not only point estimates but also full distributions over possible outcomes, giving us a richer understanding of the model’s uncertainty.
Training a Bayesian neural network involves not only optimizing the network’s parameters but also learning the distributions over these parameters. This process typically involves techniques such as variational inference or Markov chain Monte Carlo methods to approximate the posterior distribution over weights.
The benefits of using Bayesian neural networks are manifold. By incorporating uncertainty into our models, we can make more informed decisions in situations where data is scarce or noisy. BNNs are also robust against overfitting, as they naturally encode regularization through their probabilistic framework.
In addition, Bayesian neural networks offer a principled way to perform model averaging, combining multiple models with different parameter settings to improve overall performance. This ensemble approach can lead to more accurate predictions and better generalization to unseen data.
As researchers continue to explore the capabilities of Bayesian neural networks, we can expect further advancements in areas such as deep reinforcement learning, meta-learning, and uncertainty quantification. By harnessing the power of both neural networks and Bayesian inference, BNNs open up new possibilities for creating intelligent systems that are not only predictive but also introspective and adaptive.
Mastering Bayesian Neural Networks: 9 Essential Tips for Enhancing Prediction Accuracy and Uncertainty Quantification
- Understand the principles of Bayesian inference.
- Incorporate prior knowledge into the model using prior distributions.
- Use Bayesian neural networks to quantify uncertainty in predictions.
- Implement techniques like Markov Chain Monte Carlo (MCMC) for Bayesian inference.
- Explore variational inference methods for faster approximation of posterior distributions.
- Regularize the model with techniques like dropout to prevent overfitting.
- Consider the trade-off between computational complexity and accuracy when choosing priors.
- Experiment with different likelihood functions based on the nature of the problem.
- Stay updated on advancements in Bayesian deep learning research.
Understand the principles of Bayesian inference.
To effectively utilize Bayesian neural networks, it is crucial to have a solid understanding of the principles of Bayesian inference. Bayesian inference provides a systematic framework for updating beliefs about uncertain quantities based on observed data. By grasping these principles, one can better appreciate how Bayesian neural networks leverage probabilistic reasoning to model uncertainty and make more reliable predictions. Understanding Bayesian inference allows practitioners to interpret the results of BNNs in a meaningful way, enabling them to make informed decisions and extract valuable insights from the model’s outputs.
Incorporate prior knowledge into the model using prior distributions.
By incorporating prior knowledge into the model using prior distributions, Bayesian neural networks offer a powerful mechanism for leveraging existing information and expertise to improve the learning process. These prior distributions serve as a way to encode our beliefs about the parameters of the model before observing any data, allowing us to guide the learning process in a more informed and structured manner. By integrating prior knowledge into the model, we can not only enhance its performance but also make more reliable and interpretable predictions based on a combination of data-driven insights and domain-specific expertise.
Use Bayesian neural networks to quantify uncertainty in predictions.
Utilizing Bayesian neural networks allows for the quantification of uncertainty in predictions, providing a more comprehensive understanding of the model’s confidence levels. By assigning probability distributions to the network’s parameters, Bayesian neural networks offer a probabilistic framework that goes beyond traditional point estimates, enabling users to capture and assess uncertainty in their predictions. This capability not only enhances decision-making processes but also ensures more reliable and robust model outputs, particularly in scenarios where uncertainty plays a crucial role in determining the reliability of predictions.
Implement techniques like Markov Chain Monte Carlo (MCMC) for Bayesian inference.
To enhance the capabilities of Bayesian neural networks, implementing techniques like Markov Chain Monte Carlo (MCMC) for Bayesian inference can be highly beneficial. MCMC methods provide a powerful way to approximate complex posterior distributions over the network’s parameters, allowing for more accurate and robust uncertainty estimation. By leveraging MCMC in the training process, Bayesian neural networks can better capture the inherent uncertainties in data and make more reliable predictions, ultimately improving the model’s performance and generalization capabilities.
Explore variational inference methods for faster approximation of posterior distributions.
To enhance the efficiency and speed of approximating posterior distributions in Bayesian neural networks, it is recommended to delve into variational inference methods. By exploring variational inference techniques, such as mean-field approximation or stochastic variational inference, researchers and practitioners can achieve faster and more scalable approximations of the posterior distribution over network weights. These methods offer a computationally efficient way to optimize the model’s parameters while simultaneously learning an approximate posterior distribution. Embracing variational inference in Bayesian neural networks can significantly streamline the training process and enable more effective uncertainty quantification in predictive modeling tasks.
Regularize the model with techniques like dropout to prevent overfitting.
To enhance the performance and generalization of a Bayesian neural network, it is crucial to incorporate regularization techniques such as dropout. By randomly deactivating a fraction of neurons during training, dropout helps prevent overfitting by promoting robustness and reducing the reliance on specific nodes. This regularization method encourages the network to learn more generalized features and patterns from the data, leading to improved model performance on unseen examples. Incorporating dropout in a Bayesian neural network can effectively enhance its ability to make accurate predictions while mitigating the risk of overfitting to the training data.
Consider the trade-off between computational complexity and accuracy when choosing priors.
When working with Bayesian neural networks, it is crucial to carefully consider the trade-off between computational complexity and accuracy when selecting priors for the model. The choice of priors can significantly impact the performance and behavior of the network, influencing factors such as convergence speed, generalization ability, and robustness to noise. While more complex priors may better capture the underlying structure of the data, they can also increase computational costs and require more sophisticated inference techniques. On the other hand, simpler priors may lead to faster computations but could result in a less accurate representation of the true distribution. Finding the right balance between computational efficiency and modeling accuracy is essential in maximizing the effectiveness of Bayesian neural networks for a given task.
Experiment with different likelihood functions based on the nature of the problem.
When working with Bayesian neural networks, it is crucial to experiment with different likelihood functions that are tailored to the specific nature of the problem at hand. The choice of likelihood function plays a significant role in determining how well the model captures the underlying patterns in the data and makes accurate predictions. By selecting an appropriate likelihood function that aligns with the characteristics of the problem, such as Gaussian, categorical, or Poisson distributions, researchers can enhance the model’s performance and ensure that it effectively captures the nuances of the data. This flexibility in choosing likelihood functions allows for a more customized and precise approach to modeling complex real-world problems using Bayesian neural networks.
Stay updated on advancements in Bayesian deep learning research.
To fully leverage the potential of Bayesian neural networks, it is crucial to stay informed and up-to-date on the latest advancements in Bayesian deep learning research. By keeping abreast of new developments, techniques, and methodologies in this rapidly evolving field, you can enhance your understanding of how to effectively implement and optimize BNNs for various applications. Continuous learning and staying connected with the broader research community will not only help you stay at the forefront of innovation but also inspire new ideas and approaches to push the boundaries of Bayesian neural network technology.