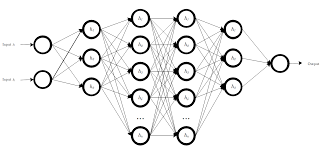
Neural networks have revolutionized the field of artificial intelligence and machine learning, enabling computers to learn complex patterns and make decisions in a way that mimics the human brain. Among the various types of neural networks, the XOR neural network stands out as a classic example that showcases the power of these systems.
The XOR (exclusive OR) neural network is a simple yet significant model that demonstrates the capability of neural networks to solve non-linear problems. The XOR operation is a logical operation that outputs true only when inputs differ. While this may seem straightforward for humans, it poses a challenge for traditional linear models.
What makes the XOR neural network special is its ability to learn and represent non-linear relationships between input and output data. By using hidden layers and activation functions, such as sigmoid or ReLU, the network can capture complex patterns and make accurate predictions for XOR operations.
Training an XOR neural network involves adjusting weights and biases through a process called backpropagation, where errors are propagated back through the network to update parameters. This iterative process allows the network to learn the underlying patterns in the data and improve its performance over time.
While the XOR neural network may seem like a basic example, its implications are far-reaching. It serves as a foundation for more advanced neural network architectures used in tasks such as image recognition, natural language processing, and autonomous driving. By understanding how a simple XOR network operates, researchers and developers can build more sophisticated models to tackle real-world challenges.
In conclusion, the XOR neural network exemplifies the versatility and power of neural networks in solving complex problems that traditional algorithms struggle with. As technology continues to advance, we can expect neural networks to play an increasingly important role in shaping our future by enabling machines to learn, adapt, and make intelligent decisions.
Mastering XOR Neural Networks: 8 Key Tips for Effective Learning and Optimization
- Understand that XOR is a non-linearly separable problem.
- Use at least one hidden layer in the neural network to learn the XOR function.
- Ensure that the activation functions used are capable of modeling non-linear relationships (e.g., ReLU, sigmoid).
- Consider using a sufficient number of neurons in the hidden layer to capture complex patterns.
- Train the neural network with an appropriate optimizer and loss function for binary classification tasks.
- Normalize input data to improve convergence during training.
- Monitor training progress by evaluating loss and accuracy metrics on a validation set.
- Experiment with different architectures and hyperparameters to optimize performance.
Understand that XOR is a non-linearly separable problem.
To grasp the concept of XOR neural networks, it is crucial to recognize that XOR is a non-linearly separable problem. Unlike linearly separable problems where a straight line can divide the classes, XOR requires a more complex approach due to its non-linear nature. This means that traditional linear models are insufficient for solving XOR operations, highlighting the need for neural networks with hidden layers and activation functions to capture the intricate relationships between inputs and outputs. By understanding the non-linear separability of XOR, one can appreciate the significance of neural networks in handling such intricate patterns and making accurate predictions.
Use at least one hidden layer in the neural network to learn the XOR function.
To effectively learn the XOR function, it is crucial to incorporate at least one hidden layer in the neural network. The hidden layer allows the network to capture and represent the non-linear relationships present in the XOR operation, enabling it to learn and make accurate predictions. By introducing this hidden layer and utilizing appropriate activation functions, the neural network gains the capacity to navigate complex patterns and improve its ability to solve the XOR problem efficiently. This strategic use of hidden layers enhances the network’s learning capabilities and demonstrates the importance of architectural design in achieving successful outcomes in neural network training tasks like XOR function approximation.
Ensure that the activation functions used are capable of modeling non-linear relationships (e.g., ReLU, sigmoid).
To effectively implement an XOR neural network, it is crucial to select activation functions that can capture and represent non-linear relationships in the data. Activation functions like ReLU and sigmoid are essential for enabling the network to learn complex patterns and make accurate predictions for XOR operations. By incorporating these activation functions, the neural network can effectively model the intricate interactions between input variables, allowing it to overcome the inherent non-linearity of XOR operations and improve its overall performance.
Consider using a sufficient number of neurons in the hidden layer to capture complex patterns.
When working with an XOR neural network, it is crucial to consider using a sufficient number of neurons in the hidden layer to effectively capture complex patterns. By increasing the number of neurons, the network gains the capacity to learn and represent intricate relationships within the data, allowing for more accurate predictions and improved performance. This approach enhances the network’s ability to handle non-linear problems like XOR operations, demonstrating the importance of thoughtful design choices in optimizing neural network architectures for optimal results.
Train the neural network with an appropriate optimizer and loss function for binary classification tasks.
When training a XOR neural network for binary classification tasks, it is crucial to select an appropriate optimizer and loss function to ensure optimal performance. The choice of optimizer, such as Adam or SGD, can greatly impact the speed and efficiency of the training process by adjusting the weights and biases of the network. Additionally, selecting a suitable loss function, such as binary cross-entropy, helps the network accurately measure its performance and make necessary adjustments during training. By carefully choosing the optimizer and loss function, developers can enhance the XOR neural network’s ability to learn complex patterns and make accurate predictions for binary classification tasks.
Normalize input data to improve convergence during training.
Normalizing input data is a crucial tip for improving convergence during training of an XOR neural network. By scaling the input data to a consistent range, such as between 0 and 1 or -1 and 1, we can prevent large variations in the data from affecting the learning process. This helps the network converge faster and more effectively by ensuring that all features contribute equally to the training process. Normalization also helps prevent issues such as vanishing or exploding gradients, which can hinder the network’s ability to learn complex patterns. Overall, normalizing input data is a simple yet powerful technique that can significantly enhance the performance and efficiency of an XOR neural network.
Monitor training progress by evaluating loss and accuracy metrics on a validation set.
Monitoring the training progress of an XOR neural network is crucial for ensuring its effectiveness and performance. By evaluating loss and accuracy metrics on a validation set throughout the training process, developers can gain valuable insights into how well the network is learning and generalizing patterns. The loss metric indicates how well the network is minimizing errors during training, while accuracy provides a measure of how effectively it is making correct predictions. By tracking these metrics on a separate validation set, developers can identify overfitting, adjust model parameters, and optimize the network for better performance on unseen data. This proactive approach to monitoring training progress helps ensure that the XOR neural network learns effectively and produces accurate results in real-world applications.
Experiment with different architectures and hyperparameters to optimize performance.
To maximize the performance of an XOR neural network, it is crucial to experiment with various architectures and hyperparameters. By exploring different network structures, such as adjusting the number of hidden layers, neurons per layer, and activation functions, researchers can fine-tune the model to better capture the underlying patterns in the data. Additionally, optimizing hyperparameters like learning rate, batch size, and regularization techniques can significantly impact the network’s training process and overall accuracy. Through systematic experimentation and analysis of results, developers can uncover the most effective configurations that enhance the XOR neural network’s performance and unlock its full potential in solving complex non-linear problems.