The Power of Convex Neural Networks in Machine Learning
Neural networks have revolutionized the field of machine learning, enabling computers to learn complex patterns and make intelligent decisions. Among the various types of neural networks, convex neural networks stand out for their unique properties and capabilities.
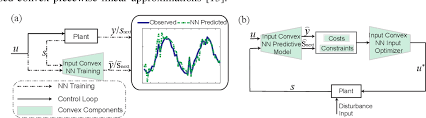
Convex neural networks are a special class of neural networks that have convex activation functions. Unlike traditional neural networks that may have non-convex activation functions, convex neural networks offer several advantages that make them particularly powerful in certain applications.
Key Features of Convex Neural Networks:
- Guaranteed Global Optima: Convex neural networks have a single global optimum solution, which makes training more stable and efficient compared to non-convex models that may get stuck in local minima.
- Efficient Training: Due to their convex nature, these networks can be trained using convex optimization techniques, leading to faster convergence and better generalization performance.
- Interpretability: Convex neural networks often produce more interpretable results, making it easier for researchers and practitioners to understand how the model arrives at its predictions.
- Robustness: Convex neural networks are less prone to overfitting and can generalize well to unseen data, making them suitable for a wide range of real-world applications.
Applications of Convex Neural Networks:
The unique properties of convex neural networks make them well-suited for various machine learning tasks, including:
- Regression Analysis: Convex neural networks are effective for modeling continuous relationships between input and output variables in regression tasks.
- Classification Problems: They perform well in classification tasks where clear decision boundaries are needed to separate different classes.
- Anomaly Detection: Convex neural networks excel at detecting anomalies or outliers in data by capturing subtle patterns that deviate from normal behavior.
- Data Clustering: They can be used for clustering data points into distinct groups based on similarities in feature space.
In conclusion, convex neural networks represent a promising approach in machine learning due to their unique characteristics and versatile applications. By leveraging the power of convex optimization and interpretability, these networks offer a valuable tool for researchers and practitioners seeking efficient and reliable solutions to complex learning problems.
5 Essential Tips for Optimizing and Understanding Convex Neural Networks
- Convex neural networks have a single global minimum, making optimization easier compared to non-convex networks.
- Regularization techniques such as L1 or L2 regularization can help prevent overfitting in convex neural networks.
- Convex neural networks are more interpretable due to their convex nature, allowing for better understanding of the model’s behavior.
- Choosing appropriate activation functions like ReLU can improve the performance of convex neural networks.
- When dealing with large datasets, convex neural networks may offer faster convergence and training times compared to non-convex models.
Convex neural networks have a single global minimum, making optimization easier compared to non-convex networks.
Convex neural networks possess a distinctive advantage in optimization due to their property of having a single global minimum. This characteristic simplifies the training process significantly when compared to non-convex networks, which are prone to getting trapped in local minima during optimization. The presence of a single global minimum in convex neural networks ensures that the optimization algorithm converges to the most optimal solution efficiently and effectively, making them an appealing choice for tasks where stable and reliable optimization is crucial.
Regularization techniques such as L1 or L2 regularization can help prevent overfitting in convex neural networks.
Regularization techniques, such as L1 or L2 regularization, play a crucial role in preventing overfitting in convex neural networks. By adding a regularization term to the loss function during training, these techniques help control the complexity of the model and discourage the network from fitting noise in the training data. In the context of convex neural networks, regularization acts as a powerful tool to improve generalization performance, enhance model robustness, and ensure that the network can effectively capture relevant patterns in the data without overemphasizing outliers or irrelevant features.
Convex neural networks are more interpretable due to their convex nature, allowing for better understanding of the model’s behavior.
Convex neural networks are known for their enhanced interpretability, a key advantage stemming from their convex nature. This inherent property enables researchers and practitioners to gain deeper insights into the inner workings of the model, facilitating a clearer understanding of how the network processes information and makes decisions. By offering transparency in its behavior, convex neural networks empower users to analyze and interpret the reasoning behind the model’s predictions, ultimately enhancing trust and confidence in its outcomes.
Choosing appropriate activation functions like ReLU can improve the performance of convex neural networks.
Choosing appropriate activation functions like Rectified Linear Unit (ReLU) can significantly enhance the performance of convex neural networks. Activation functions play a crucial role in shaping the behavior and learning capabilities of neural networks. ReLU, known for its simplicity and effectiveness, helps convex neural networks achieve faster convergence, better generalization, and improved computational efficiency. By selecting the right activation functions, such as ReLU, practitioners can optimize the network’s performance and unlock its full potential in various machine learning tasks.
When dealing with large datasets, convex neural networks may offer faster convergence and training times compared to non-convex models.
When working with large datasets, leveraging convex neural networks can be advantageous due to their potential for faster convergence and training times in comparison to non-convex models. The convex nature of these networks allows for efficient optimization using convex techniques, leading to more stable training processes and quicker convergence to global optima. This characteristic makes convex neural networks particularly well-suited for handling the complexities of large datasets, enabling researchers and practitioners to train models more effectively and extract valuable insights from vast amounts of data in a timely manner.