Permutation Invariant Neural Network: Revolutionizing Pattern Recognition
Pattern recognition is a fundamental task in various fields, from image and speech processing to natural language understanding. Traditional neural networks excel at recognizing patterns in fixed input sequences. However, when the order of input elements is irrelevant, such networks struggle to capture the underlying patterns effectively.
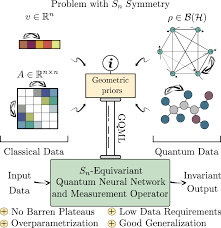
This is where permutation invariant neural networks come into play. These innovative neural networks are designed to be invariant to the order of input elements, making them ideal for tasks where the arrangement of data points does not matter.
One of the key features of permutation invariant neural networks is their ability to aggregate information from all input elements simultaneously. Instead of relying on sequential processing, these networks leverage permutation-invariant layers that combine information from different input permutations in a consistent manner.
By incorporating permutation invariance into the network architecture, researchers have achieved remarkable success in various applications. For instance, in image recognition tasks where the spatial arrangement of pixels is irrelevant, permutation invariant neural networks have demonstrated superior performance compared to traditional convolutional neural networks.
Moreover, permutation invariant neural networks have shown promise in natural language processing tasks such as sentiment analysis and text classification. By treating words or tokens as interchangeable entities, these networks can effectively capture semantic relationships within text data without being influenced by word order.
The potential applications of permutation invariant neural networks are vast and continue to expand as researchers explore new ways to leverage their unique capabilities. From analyzing molecular structures in chemistry to processing financial data for predictive modeling, these versatile networks offer a new paradigm for pattern recognition across diverse domains.
In conclusion, permutation invariant neural networks represent a significant advancement in the field of deep learning, enabling more robust and flexible pattern recognition capabilities. As researchers continue to refine and innovate upon this technology, we can expect further breakthroughs that will shape the future of artificial intelligence and machine learning.
6 Essential Tips for Building Permutation Invariant Neural Networks
- Use symmetric functions to aggregate features across permutations of inputs.
- Ensure that the network architecture is permutation invariant.
- Consider using max or sum pooling layers to achieve permutation invariance.
- Normalize input data to make the model more robust to different permutations.
- Explore graph neural networks for handling permutation invariance in graph-structured data.
- Regularize the model by incorporating equivariance constraints.
Use symmetric functions to aggregate features across permutations of inputs.
To enhance the performance of permutation invariant neural networks, it is recommended to utilize symmetric functions for aggregating features across permutations of inputs. By incorporating symmetric functions into the network architecture, information from different input permutations can be effectively combined in a consistent and unbiased manner. This approach ensures that the network is capable of capturing and leveraging patterns regardless of the order of input elements, thereby enhancing its overall robustness and accuracy in pattern recognition tasks.
Ensure that the network architecture is permutation invariant.
To maximize the effectiveness of a permutation invariant neural network, it is crucial to ensure that the network architecture itself is designed to be permutation invariant. This means incorporating layers and mechanisms that can aggregate information from input elements regardless of their order. By structuring the network in a way that is invariant to permutations, we can harness the full potential of this innovative approach to pattern recognition, enabling the network to effectively capture and process information without being influenced by the sequence in which data points are presented.
Consider using max or sum pooling layers to achieve permutation invariance.
When implementing a permutation invariant neural network, it is advisable to consider incorporating max or sum pooling layers in the architecture. These pooling layers play a crucial role in achieving permutation invariance by aggregating information from all input elements without considering their order. By using max pooling, the network selects the maximum value from each feature dimension across different permutations, while sum pooling calculates the sum of values. Both techniques help capture essential patterns and features from the input data, regardless of their arrangement, making them valuable tools for enhancing the network’s performance in tasks where order does not matter.
Normalize input data to make the model more robust to different permutations.
One effective tip for enhancing the performance of a permutation invariant neural network is to normalize the input data. By normalizing the input data, we can ensure that the model remains robust to different permutations of the input elements. Normalization helps to standardize the range and distribution of input features, making it easier for the network to learn and generalize patterns effectively across various permutations. This preprocessing step can improve the stability and convergence of the model, ultimately leading to more reliable and accurate predictions in real-world applications.
Explore graph neural networks for handling permutation invariance in graph-structured data.
Graph neural networks offer a compelling solution for addressing permutation invariance in graph-structured data. By leveraging the inherent structure and relationships within graphs, these networks can effectively capture and process information without being influenced by the order of nodes or edges. This makes them well-suited for tasks where the arrangement of data points is arbitrary, such as social network analysis, molecular structure prediction, and recommendation systems. Exploring graph neural networks presents a promising avenue for enhancing the capabilities of permutation invariant neural networks and unlocking new possibilities in pattern recognition and data analysis within graph data domains.
Regularize the model by incorporating equivariance constraints.
To enhance the performance and generalization of a permutation invariant neural network, it is advisable to regularize the model by integrating equivariance constraints. By imposing equivariance constraints, the network is encouraged to maintain consistency in its predictions when the input data undergoes certain transformations or permutations. This regularization technique helps the model learn more robust and stable representations of the data, leading to improved accuracy and reliability in various pattern recognition tasks.