Kohonen Neural Network: Understanding Self-Organizing Maps
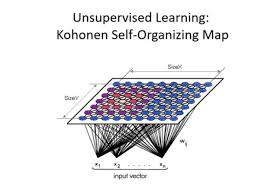
The Kohonen neural network, also known as a self-organizing map (SOM), is a type of artificial neural network that is used for clustering and visualizing high-dimensional data. Developed by Finnish professor Teuvo Kohonen in the 1980s, this powerful tool has found applications in various fields such as data mining, image processing, and pattern recognition.
Unlike traditional neural networks that are used for supervised learning tasks, a Kohonen network is unsupervised and relies on a competitive learning process to organize input data based on similarity. The network consists of nodes arranged in a two-dimensional grid, with each node representing a cluster or category.
One of the key features of a Kohonen network is its ability to learn the underlying structure of data without explicit labels or class information. During training, the network adjusts its weights to map input vectors onto the grid in such a way that similar inputs are placed close together while dissimilar inputs are placed farther apart.
This self-organizing property allows the Kohonen network to create a topological map of the input space, where neighboring nodes on the grid represent similar features. This makes it easier to visualize and interpret complex data patterns and relationships.
Applications of Kohonen networks include image compression, data visualization, and clustering analysis. For example, in image processing, a SOM can be used to reduce the dimensionality of an image while preserving its essential features. In data mining, it can help identify clusters or groups within large datasets based on similarity.
In conclusion, the Kohonen neural network offers a powerful tool for exploring and understanding complex datasets through unsupervised learning. Its ability to organize high-dimensional data into meaningful patterns makes it an invaluable resource for researchers and practitioners across various disciplines.
5 Essential Tips for Mastering Kohonen Neural Networks
- Start with a small network size before scaling up for better understanding.
- Normalize input data to ensure all features contribute equally to the training process.
- Experiment with different learning rates and neighborhood functions to optimize network performance.
- Visualize the weight vectors in the output space to interpret how the network clusters input data.
- Monitor the quantization error and topographic error during training to assess convergence and quality of the map.
Start with a small network size before scaling up for better understanding.
To better understand the Kohonen neural network, it is advisable to start with a small network size before scaling up. By beginning with a smaller network, you can grasp the fundamental concepts and mechanisms of self-organizing maps more effectively. This approach allows you to observe how the network organizes and clusters data in a simpler context before dealing with larger and more complex datasets. Starting small provides a solid foundation for building upon and scaling up the network size later on, leading to a clearer understanding of how the Kohonen neural network operates and its applications in various fields.
Normalize input data to ensure all features contribute equally to the training process.
When working with a Kohonen neural network, it is essential to normalize the input data to ensure that all features contribute equally to the training process. Normalization involves scaling the input values so that they fall within a similar range, preventing features with larger magnitudes from dominating the learning process. By normalizing the data, each feature has an equal opportunity to influence the network’s weight adjustments during training, leading to a more balanced and effective self-organizing map that accurately reflects the underlying patterns in the data.
Experiment with different learning rates and neighborhood functions to optimize network performance.
To optimize the performance of a Kohonen neural network, it is recommended to experiment with different learning rates and neighborhood functions. The learning rate determines how much the weights of the network are adjusted during training, while the neighborhood function defines the influence of neighboring nodes on the weight updates. By varying these parameters, researchers and practitioners can fine-tune the network’s behavior to achieve better convergence and more accurate clustering results. This experimentation process allows for customization of the network based on specific data characteristics and problem requirements, ultimately enhancing its performance in various applications.
Visualize the weight vectors in the output space to interpret how the network clusters input data.
To gain insights into how the Kohonen neural network clusters input data, a valuable tip is to visualize the weight vectors in the output space. By examining the arrangement of these weight vectors on the grid, one can interpret how similar input data points are grouped together based on their features. This visualization technique provides a clear representation of how the network organizes and categorizes data, allowing for a better understanding of the underlying patterns and relationships within the dataset.
Monitor the quantization error and topographic error during training to assess convergence and quality of the map.
Monitoring the quantization error and topographic error during training is crucial when working with a Kohonen neural network. These metrics provide valuable insights into the convergence and quality of the map being generated. The quantization error measures how well the network’s nodes represent the input data, while the topographic error evaluates the preservation of the input data’s spatial relationships on the map. By tracking these errors throughout the training process, practitioners can assess the network’s progress, make necessary adjustments, and ensure that the resulting map accurately reflects the underlying structure of the data.