Polynomial Neural Network: A Powerful Tool for Nonlinear Function Approximation
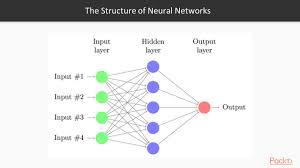
Neural networks have revolutionized the field of machine learning by enabling complex pattern recognition and data processing tasks. Among the various types of neural networks, the polynomial neural network stands out as a versatile and effective tool for approximating nonlinear functions.
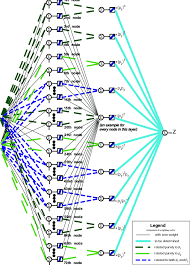
Unlike traditional neural networks that use linear activation functions, polynomial neural networks employ polynomial activation functions to model complex relationships between inputs and outputs. This allows them to capture nonlinear patterns in data more effectively, making them ideal for tasks such as regression, classification, and function approximation.
The key advantage of polynomial neural networks lies in their ability to represent a wide range of functions with high accuracy. By using higher-degree polynomials in their activation functions, these networks can capture intricate nonlinearities that may be missed by simpler models.
Another benefit of polynomial neural networks is their flexibility in handling different types of data. Whether the input-output relationship is linear, quadratic, cubic, or even higher-order, these networks can adapt to the complexity of the underlying function and learn the optimal parameters for accurate prediction.
Furthermore, polynomial neural networks are robust against overfitting, thanks to their ability to generalize well on unseen data. By controlling the complexity of the polynomials used in the network architecture, practitioners can strike a balance between model complexity and generalization performance.
In conclusion, polynomial neural networks offer a powerful framework for nonlinear function approximation in machine learning tasks. With their capacity to model complex relationships and adapt to diverse data patterns, these networks are valuable tools for researchers and practitioners seeking accurate and flexible solutions in data analysis and predictive modeling.
Understanding Polynomial Neural Networks: Key FAQs Answered
- What are neural networks used for?
- Are neural networks polynomial time?
- What are polynomial neural networks?
- Which of the following will reduce the Overfitting in a neural network?
- Would you use polynomial features in neural network?
- What is polynomial in networking?
What are neural networks used for?
Neural networks are versatile and powerful tools used in various fields for a wide range of applications. One common application of neural networks is in pattern recognition, where they excel at identifying complex patterns and relationships in data. They are also widely used in image and speech recognition, natural language processing, financial forecasting, medical diagnosis, and many other tasks that involve processing large amounts of data to make predictions or classifications. Neural networks have proven to be effective in solving problems that are difficult for traditional algorithms to handle, making them indispensable in modern artificial intelligence and machine learning applications.
Are neural networks polynomial time?
The question of whether neural networks are polynomial time is a common one in the field of computational complexity theory. While neural networks themselves are not inherently polynomial time algorithms, the training and inference processes involved in using neural networks can exhibit polynomial time complexity under certain conditions. The complexity of neural networks typically depends on factors such as the network architecture, the size of the dataset, and the specific learning algorithm employed. Researchers continue to explore ways to optimize neural network computations and improve their efficiency to better understand and harness their computational capabilities.
What are polynomial neural networks?
Polynomial neural networks are a type of neural network architecture that utilizes polynomial activation functions to model complex nonlinear relationships between input and output data. Unlike traditional neural networks that rely on linear activation functions, polynomial neural networks can capture intricate nonlinear patterns more effectively, making them well-suited for tasks such as regression, classification, and function approximation. By leveraging higher-degree polynomials in their activation functions, these networks can represent a wide range of functions with high accuracy, offering a versatile and powerful tool for handling diverse data types and complexities in machine learning applications.
Which of the following will reduce the Overfitting in a neural network?
To reduce overfitting in a neural network, several strategies can be implemented. One effective approach is to introduce regularization techniques such as L1 or L2 regularization, which add penalty terms to the loss function to discourage overly complex models. Another method is to use dropout, where random neurons are temporarily removed during training to prevent the network from relying too heavily on specific nodes. Additionally, increasing the size of the training dataset or applying data augmentation techniques can help expose the model to a wider range of examples, improving its generalization ability. Finally, early stopping, which halts training when performance on a validation set starts to decline, can prevent the network from memorizing noise in the data and focus on learning meaningful patterns instead.
Would you use polynomial features in neural network?
When considering whether to use polynomial features in a neural network, it is important to evaluate the complexity of the underlying data and the nature of the relationships between inputs and outputs. Polynomial features can be beneficial in capturing nonlinear patterns and interactions that may exist in the data, especially when traditional linear models are insufficient. By incorporating polynomial features into a neural network architecture, it becomes possible to model more intricate relationships and improve the network’s ability to approximate complex functions accurately. However, it is essential to strike a balance between model complexity and overfitting, as excessively high-degree polynomials can lead to increased computational costs and potential performance degradation on unseen data. Therefore, the decision to use polynomial features in a neural network should be guided by a thorough understanding of the data characteristics and modeling objectives.
What is polynomial in networking?
In the context of neural networks, a polynomial refers to a type of mathematical function used as an activation function within the network architecture. Specifically, a polynomial activation function introduces nonlinearities by incorporating terms of different degrees, such as x, x^2, x^3, and so on. This allows the neural network to capture complex relationships between input variables and model intricate patterns in the data more effectively. By utilizing polynomials in networking, researchers and practitioners can enhance the network’s ability to approximate nonlinear functions and improve its performance in tasks such as regression, classification, and function approximation.