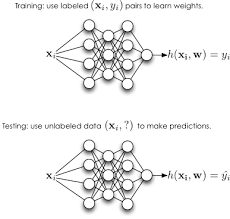
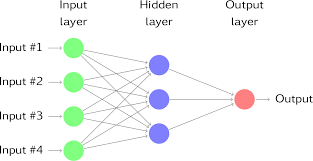
Linear Regression Neural Network: Combining Simplicity with Power
Linear regression and neural networks are two widely used techniques in the field of machine learning. While linear regression is known for its simplicity and interpretability, neural networks are renowned for their ability to capture complex patterns in data. In recent years, researchers and practitioners have been exploring the combination of these two techniques to create a powerful hybrid model known as the linear regression neural network.
At its core, a linear regression neural network is a neural network that includes one or more linear regression layers. These layers serve as the foundation of the network, providing a simple yet effective way to model relationships between input features and output targets. By combining the strengths of linear regression with the flexibility of neural networks, this hybrid model can achieve superior performance in various prediction tasks.
One key advantage of the linear regression neural network is its ability to handle both linear and nonlinear relationships in data. The linear regression layers can capture simple linear patterns, while the additional nonlinear layers in the neural network can learn more complex patterns and interactions among features. This enables the model to adapt to a wide range of data distributions and make accurate predictions across different scenarios.
Another benefit of this hybrid approach is its interpretability. Unlike traditional black-box neural networks, the linear regression neural network allows users to examine the coefficients assigned to each input feature in the linear regression layers. This transparency can help users understand how each feature contributes to the prediction and gain insights into the underlying relationships within the data.
In practice, linear regression neural networks have been successfully applied in various fields, including finance, healthcare, marketing, and more. Researchers have found that this hybrid model can outperform standalone linear regression or neural network models in terms of predictive accuracy and generalization capability.
As machine learning continues to evolve, the exploration of innovative model architectures like the linear regression neural network highlights the importance of combining different techniques to harness their complementary strengths. By leveraging both simplicity and power, this hybrid approach opens up new possibilities for solving complex real-world problems with efficiency and effectiveness.
Understanding Linear Regression in Neural Networks: 7 Frequently Asked Questions
- Is linear regression A special case of neural network?
- Can neural networks be used for linear regression?
- Is a neural network non-linear regression?
- Can we use neural network for linear regression?
- What is linear regression in deep learning?
- Is linear regression a single layer neural network?
- Can tensorflow do linear regression?
Is linear regression A special case of neural network?
The question of whether linear regression is a special case of a neural network is a common one in the field of machine learning. In essence, linear regression can be viewed as a simplified form of a neural network with no hidden layers or activation functions. While linear regression focuses on modeling linear relationships between input features and output targets, neural networks offer more flexibility by incorporating nonlinear transformations through hidden layers. Despite their differences, linear regression can indeed be considered a special case of a neural network, highlighting the foundational principles shared between these two techniques in capturing and modeling data patterns.
Can neural networks be used for linear regression?
Yes, neural networks can be used for linear regression. While neural networks are commonly associated with complex nonlinear relationships and tasks such as image recognition and natural language processing, they can also be applied to simpler tasks like linear regression. In fact, a neural network with just one neuron and a linear activation function can perform linear regression effectively. By adjusting the weights and biases of the neuron through training, the neural network can learn to model the relationship between input features and output targets in a linear fashion. This flexibility showcases the versatility of neural networks, demonstrating their capability to handle a wide range of machine learning tasks, including linear regression.
Is a neural network non-linear regression?
In the context of machine learning, it is important to clarify that while neural networks are often associated with non-linear regression due to their ability to model complex relationships in data, not all neural networks are inherently non-linear. In fact, the term “neural network” refers to a broad class of models that can include both linear and non-linear components. Traditional feedforward neural networks with only linear activation functions can perform linear regression, capturing simple linear patterns in data. However, to handle more intricate patterns and nonlinear relationships, additional non-linear activation functions are typically introduced in the network layers. Therefore, while neural networks have the capacity for non-linear regression, their specific capabilities depend on the architecture and activation functions used within the model.
Can we use neural network for linear regression?
The frequently asked question about using neural networks for linear regression often arises due to the perception that neural networks are primarily suited for complex, nonlinear problems. However, it is important to note that neural networks can indeed be used for linear regression tasks effectively. By incorporating a single neuron or layer with linear activation function, a neural network can essentially function as a linear regression model. This approach not only allows for the utilization of neural network capabilities such as automatic feature learning and optimization but also provides flexibility in handling both linear and nonlinear relationships in the data. Therefore, employing a neural network for linear regression can offer advantages in terms of adaptability and performance, making it a viable and beneficial choice for various predictive modeling tasks.
What is linear regression in deep learning?
Linear regression in deep learning refers to the use of linear models within neural networks to perform regression tasks. In this context, linear regression serves as a foundational building block that helps capture and model the relationships between input features and output targets. By incorporating linear regression layers into deep learning architectures, researchers and practitioners can leverage the simplicity and interpretability of linear models while benefiting from the flexibility and power of neural networks to handle complex data patterns. This combination allows for more effective modeling of continuous variables and prediction tasks in deep learning applications.
Is linear regression a single layer neural network?
The question of whether linear regression can be considered a single-layer neural network is a common topic of discussion in the field of machine learning. While linear regression and single-layer neural networks share similarities in their structure and functionality, there are key differences that distinguish them. Linear regression is a simple and interpretable model that aims to establish a linear relationship between input features and output targets, typically using a closed-form solution or optimization algorithm. On the other hand, a single-layer neural network, although also consisting of input nodes and an output node like linear regression, incorporates activation functions and weights that allow it to capture nonlinear patterns in the data. Thus, while linear regression can be viewed as a special case of a neural network with no hidden layers, the inclusion of activation functions in neural networks enables them to model more complex relationships beyond linearity.
Can tensorflow do linear regression?
Yes, TensorFlow is a versatile and powerful machine learning library that can indeed perform linear regression tasks. With TensorFlow, users can easily implement linear regression models using its built-in functionalities for defining computational graphs, optimizing parameters, and making predictions. By leveraging TensorFlow’s flexible architecture and efficient computation capabilities, developers and researchers can create and train linear regression models with ease, allowing for accurate prediction of continuous values based on input features. Whether it’s a simple linear regression or a more complex neural network incorporating linear regression layers, TensorFlow provides the tools necessary to tackle various regression tasks effectively.