The Multilayer Perceptron Neural Network: Understanding the Basics
Neural networks have revolutionized the field of artificial intelligence and machine learning, enabling computers to learn from data and make decisions in a way that mimics the human brain. One of the most common types of neural networks is the multilayer perceptron (MLP), which is widely used for a variety of tasks such as image recognition, natural language processing, and financial forecasting.
Structure of a Multilayer Perceptron
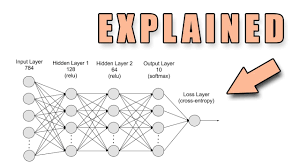
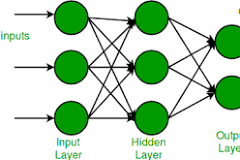
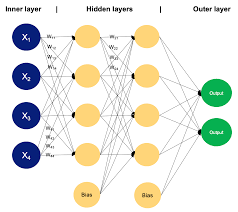
The multilayer perceptron consists of multiple layers of nodes, or neurons, organized in a hierarchical structure. The network is composed of an input layer, one or more hidden layers, and an output layer. Each neuron in a layer is connected to every neuron in the following layer through weighted connections.
Working Principle
During the training phase, the MLP learns by adjusting the weights of these connections based on input data and expected output. This process involves forward propagation, where input data is passed through the network to generate predictions, and backward propagation (backpropagation), where errors are calculated and used to update the weights through optimization algorithms like gradient descent.
Activation Function
Each neuron in an MLP uses an activation function to introduce non-linearity into the network. Common activation functions include sigmoid, tanh, ReLU (Rectified Linear Unit), and softmax functions. These functions help the network learn complex patterns and relationships in data that would be impossible with just linear transformations.
Applications of Multilayer Perceptrons
Due to their flexibility and capability to learn complex patterns, multilayer perceptrons are used in various fields such as computer vision for image classification, speech recognition for natural language processing tasks, financial modeling for predicting stock prices, and many more. Their ability to handle large amounts of data and adapt to different problem domains makes them a versatile choice for many machine learning applications.
Conclusion
The multilayer perceptron neural network is a powerful tool in the realm of artificial intelligence and machine learning. By leveraging its hierarchical structure, non-linear activation functions, and training algorithms like backpropagation, researchers and developers can build sophisticated models that can tackle a wide range of complex tasks with remarkable accuracy and efficiency.
Unlocking the Mysteries of Multilayer Perceptron Neural Networks: A Guide to Structure, Function, and Applications
- What is a multilayer perceptron neural network?
- How does a multilayer perceptron neural network work?
- What are the key components of a multilayer perceptron neural network?
- What is backpropagation in the context of a multilayer perceptron neural network?
- What are common activation functions used in multilayer perceptron neural networks?
- In what applications can multilayer perceptron neural networks be used?
What is a multilayer perceptron neural network?
A multilayer perceptron neural network, often referred to as MLP, is a type of artificial neural network with multiple layers of interconnected nodes, or neurons. This network architecture consists of an input layer, one or more hidden layers, and an output layer. Each neuron in the network receives input signals, processes them using activation functions, and passes the output to neurons in the next layer. The multilayer perceptron is designed to learn complex patterns and relationships in data through training algorithms like backpropagation, where errors are calculated and used to adjust the weights of connections between neurons. This versatile neural network is widely used in various applications such as image recognition, natural language processing, and financial forecasting due to its ability to handle non-linear relationships and adapt to different problem domains effectively.
How does a multilayer perceptron neural network work?
A multilayer perceptron neural network works by processing input data through multiple layers of interconnected neurons, each layer transforming the data in a non-linear way. The network learns to make predictions by adjusting the weights of connections between neurons during training. Through a process called backpropagation, errors in predictions are calculated and used to update the weights in order to minimize these errors. This iterative learning process allows the multilayer perceptron to capture complex patterns and relationships within the data, enabling it to make accurate predictions and classifications for various tasks such as image recognition, natural language processing, and financial forecasting.
What are the key components of a multilayer perceptron neural network?
A multilayer perceptron neural network consists of several key components that define its structure and functionality. The primary components include an input layer, one or more hidden layers, and an output layer. Neurons in each layer are interconnected through weighted connections, allowing information to flow through the network during the learning process. Activation functions play a crucial role in introducing non-linearity to the network, enabling it to learn complex patterns and relationships in data. The training algorithm, typically involving forward and backward propagation, adjusts the weights of these connections based on input data and expected output to optimize the network’s performance. Together, these components form the foundation of a multilayer perceptron neural network, making it a versatile and powerful tool for various machine learning tasks.
What is backpropagation in the context of a multilayer perceptron neural network?
Backpropagation in the context of a multilayer perceptron neural network is a crucial training algorithm that enables the network to learn from its mistakes and improve its performance over time. It involves calculating the error between the predicted output and the actual output of the network, and then propagating this error backward through the network to adjust the weights of the connections between neurons. By iteratively updating these weights using optimization techniques like gradient descent, backpropagation allows the multilayer perceptron to fine-tune its parameters and optimize its ability to make accurate predictions on new, unseen data. This iterative process of error correction is essential for improving the network’s accuracy and efficiency in solving complex tasks across various domains such as image recognition, natural language processing, and financial forecasting.
What are common activation functions used in multilayer perceptron neural networks?
In multilayer perceptron neural networks, common activation functions play a crucial role in introducing non-linearity to the network, enabling it to learn complex patterns and relationships in data. Some widely used activation functions include the sigmoid function, which squashes the output between 0 and 1; the hyperbolic tangent (tanh) function, which maps values to the range of -1 to 1; the Rectified Linear Unit (ReLU) function, which sets negative values to zero and is known for its simplicity and efficiency; and the softmax function, often used in the output layer for multiclass classification tasks. Each activation function brings its own advantages and characteristics to the network, influencing its learning capability and performance in different ways.
In what applications can multilayer perceptron neural networks be used?
Multilayer perceptron neural networks find applications across various fields due to their versatility and ability to learn complex patterns from data. In the realm of computer vision, MLPs are commonly used for tasks such as image classification, object detection, and facial recognition. In natural language processing, they are employed for sentiment analysis, text classification, and language translation. Financial institutions utilize MLPs for stock market prediction, risk assessment, and fraud detection. Additionally, multilayer perceptrons are applied in healthcare for medical image analysis, disease diagnosis, and patient outcome prediction. Their adaptability and effectiveness make them a valuable tool in diverse domains where intricate data patterns need to be understood and utilized for decision-making processes.